题目内容

已知实系数方程x2+ax+2b=0的两根在(0,1)与(1,2)内，求的取值范围.

∴


解析:

设f(x)=x2+ax+2b,依题意,此函数图象与x轴两交点横坐标在(0,1)和(1,2)内,其充要条件为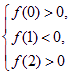即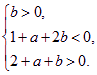

在直角坐标系中作出可行域,如下图所示.

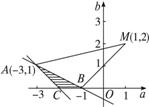
由的几何意义知△ABC内任一点P(a,b)与定点M(1,2)连线的斜率的范围即为所求.

∵, ∴

练习册系列答案
相关题目
已知实系数方程x2+ax+2b=0的一个根大于0且小于1，另一根大于1且小于2，则
b-2
a-1
的取值范围是（　　）
A、（
1
4
，1）
B、（
1
2
，1）
C、（-
1
2
，
1
4
）
D、（0，
1
3
）
已知实系数方程x2+ax+1=0的一个实根在区间（1，2）内，则a的取值范围为（　　）
A、（-2，-1）
B、(-
5
2
，-2)
C、（1，2）
D、(2，
5
2
)
已知实系数方程x2+（m+1）x+m+n+1=0的两个实根分别为x1、x2，且0＜x1＜1，x2＞1，则
n
m
的取值范围是（　　）
已知实系数方程x2+（a+1）x+a+b+1=0的两根分别为一个椭圆和一个双曲线的离心率，则
b
a
的取值范围是（　　）
A、（-2，-1）
B、(-1，-
1
2
)
C、(-2，-
1
2
)
D、（-2，+∞）
已知实系数方程x2+（m+1）x+m+n+1=0的两个实数根分别是x1，x2，且0＜x1＜1，x2＞1，则u=
m2+n2
mn
的取值范围是（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网