题目内容
17.函数f(x)=b(1-$\frac{2}{1+{2}^{x}}$)+$\frac{a•({4}^{x}-1)}{{2}^{x}}$+3(a、b为常数),若f(x)在(0,+∞)上有最大值11,则f(x)在(-∞,0)上有( )| A. | 最大值10 | B. | 最小值-5 | C. | 最小值-4 | D. | 最大值5 |
分析 设g(x)=b(1-$\frac{2}{1+{2}^{x}}$)+$\frac{a•({4}^{x}-1)}{{2}^{x}}$,判断奇偶性,可得g(x)的最值之和为0,由题意可得g(x)在(0,+∞)上有最大值8,最小值-8,进而得到所求最小值-5.
解答 解:设g(x)=b(1-$\frac{2}{1+{2}^{x}}$)+$\frac{a•({4}^{x}-1)}{{2}^{x}}$
=b•$\frac{{2}^{x}-1}{{2}^{x}+1}$+a(2x-2-x),
由g(-x)=b•$\frac{{2}^{-x}-1}{{2}^{-x}+1}$+a(2-x-2x)
=b•$\frac{1-{2}^{x}}{1+{2}^{x}}$+a(2-x-2x)=-g(x),
可得g(x)为奇函数,
由f(x)=g(x)+3,f(x)在(0,+∞)上有最大值11,
可得g(x)在(0,+∞)上有最大值11-3=8;
则g(x)在(-∞,0)上有最小值-8,
即有f(x)在(-∞,0)上有最小值为-8+3=-5.
故选B.
点评 本题考查奇函数的性质,考查函数的最值的求法,注意运用构造函数法.考查运算能力,属于中档题.

练习册系列答案
相关题目
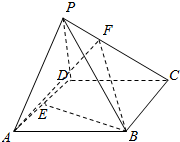 如图所示,P为?ABCD所在平面外一点,E为AD的中点,F为PC上一点,当PA∥平面EBF时,$\frac{PF}{FC}$=$\frac{1}{2}$.
如图所示,P为?ABCD所在平面外一点,E为AD的中点,F为PC上一点,当PA∥平面EBF时,$\frac{PF}{FC}$=$\frac{1}{2}$.