Question

在一次商贸会上，甲、乙两人相约同一天上午前去洽谈，若甲计划在9：00-9：40之间赶到，乙计划在9：20-10：00之间赶到，求甲比乙提前到达的概率．

Answer 1

分析：从9：00开始计时，设甲到达的时刻为x分，乙到达的时刻为y分．在xoy坐标平面内，作出试验的全部结果对应的正方形ABCD和事件“甲比乙提前到达”对应的五边形CDEFB（图中的阴影部分），算出它们的面积并利用几何概型公式加以计算，可得甲比乙提前到达的概率．

解答：解：从9：00开始计时，设甲到达的时刻为x分，乙到达的时刻为y分，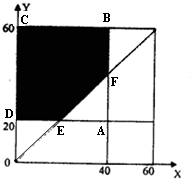
则（x，y）可以看作坐标平面内的点，
试验的全部结果所构成的区域为Ω={（x，y）|0≤x≤40，20≤y≤60}
对应的图形为正方形ABCD，其面积为S=40×（60-20）=1600．
记事件A=“甲比乙提前到达”，
构成的区域为A={（x，y）|0≤x≤40，20≤y≤60，且y＞x}，
对应的图形为五边形CDEFB，即图中的阴影部分，
其面积为S₁=S-

1

2

×20²=1400．
因此，事件A发生的概率为P=

S1

S

=

1400

1600

=

7

8

．
答：甲比乙提前到达的概率为

7

8

．

点评：本题给出两人约会的事件，求事件“甲比乙提前到达”的概率，着重考查了二元一次不等式组表示的平面区域、平面图形的面积计算和几何概型公式等知识，属于中档题．