题目内容
设函数f(x)= x2-lnx,其中a为大于零的常数。
x2-lnx,其中a为大于零的常数。
(1)当a=1时,求函数f(x)的单调区间和极值;
(2)当x∈[1,2]时,不等式f(x)>2恒成立,求a的取值范围。
 x2-lnx,其中a为大于零的常数。
x2-lnx,其中a为大于零的常数。(1)当a=1时,求函数f(x)的单调区间和极值;
(2)当x∈[1,2]时,不等式f(x)>2恒成立,求a的取值范围。
解:(1)当a=1时,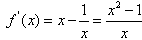
令f'(x)>0得x>1,
令f'(x)<0得0<x<1,
故函数f(x)的单调递增区间为(1,+∞),单调递减区间为(0,1)
从而f(x)在(0,+∞)上的极小值为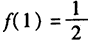
f(x)无极大值。
(2)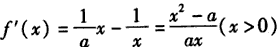
f(x)>2在[1,2]上恒成立 f(x)在[1,2]上的最小值f(x)min>2
f(x)在[1,2]上的最小值f(x)min>2
∵a>0
∴令f'(x)=0得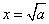
①当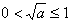 时,即0<a≤1时,函数f(x)在[1,2]上递增,
时,即0<a≤1时,函数f(x)在[1,2]上递增,
f(x)的最小值为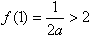
解得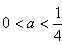 ;
;
②当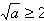 时,即
时,即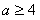 时,函数f(x)在[1,2]上递减,
时,函数f(x)在[1,2]上递减,
f(x)的最小值为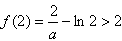 ,无解
,无解
③当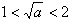 时,即1<a<4时,函数f(x)在
时,即1<a<4时,函数f(x)在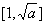 上递减,在
上递减,在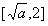 上递增,
上递增,
所以f(x)的最小值为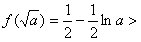 2,无解
2,无解
综上,所求a的取值范围为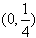 。
。
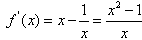
令f'(x)>0得x>1,
令f'(x)<0得0<x<1,
故函数f(x)的单调递增区间为(1,+∞),单调递减区间为(0,1)
从而f(x)在(0,+∞)上的极小值为
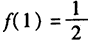
f(x)无极大值。
(2)
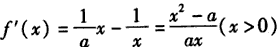
f(x)>2在[1,2]上恒成立
 f(x)在[1,2]上的最小值f(x)min>2
f(x)在[1,2]上的最小值f(x)min>2∵a>0
∴令f'(x)=0得
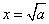
①当
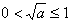 时,即0<a≤1时,函数f(x)在[1,2]上递增,
时,即0<a≤1时,函数f(x)在[1,2]上递增, f(x)的最小值为
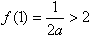
解得
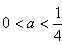 ;
;②当
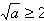 时,即
时,即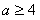 时,函数f(x)在[1,2]上递减,
时,函数f(x)在[1,2]上递减,f(x)的最小值为
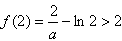 ,无解
,无解③当
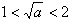 时,即1<a<4时,函数f(x)在
时,即1<a<4时,函数f(x)在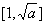 上递减,在
上递减,在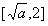 上递增,
上递增,所以f(x)的最小值为
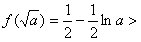 2,无解
2,无解综上,所求a的取值范围为
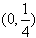 。
。
练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目