题目内容
函数 的图象( )
的图象( )
| A.关于原点对称 | B.关于点(- ,0)对称 ,0)对称 |
| C.关于y轴对称 | D.关于直线x= 对称 对称 |
B
解析试题分析:根据题意,将四个答案逐一代入可知函数值为零的即为对称中心,而对称轴处的函数值为最值,由于当(0,0)代入之后不满足,因此不是对称中心,当(- ,0)代入可知满足对称中心,成立,对于C,D可以得到代入后函数值没有取得最值,不成立,故选B.
,0)代入可知满足对称中心,成立,对于C,D可以得到代入后函数值没有取得最值,不成立,故选B.
考点:三角函数的图像与性质
点评:解决的关键是利用三角函数性质来得到对称中心的坐标,属于基础题。

练习册系列答案
相关题目
已知点 在第三象限, 则角
在第三象限, 则角 的终边在( ).
的终边在( ).
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
若函数 的图象关于直线
的图象关于直线 对称,则
对称,则 可以为( )
可以为( )
A. | B.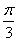 | C. | D. |
角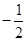 的终边过点P(4,-3),则
的终边过点P(4,-3),则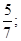 的值为( )
的值为( )
| A.4 | B.-3 | C.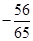 | D.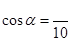 |
已知角 的终边经过点P(4,-3),则
的终边经过点P(4,-3),则 的值等于( )
的值等于( )
A. | B. | C. | D. |
如果角θ的终边经过点 那么tanθ的值是( )
那么tanθ的值是( )
A. | B. | C. | D. |
设 ,则
,则
A. | B. | C. | D. |
 一个周期内的图象上的四个点,如图所示,
一个周期内的图象上的四个点,如图所示, B为
B为 轴上的点,C为图像上的最低点,E为该函数图像的一个对称中心,B与D关于点E对称,
轴上的点,C为图像上的最低点,E为该函数图像的一个对称中心,B与D关于点E对称, 在
在 轴上的投影为
轴上的投影为 ,则
,则 的值为
的值为




 -2x)的单调增区间是[
-2x)的单调增区间是[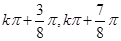 ],kÎZ
],kÎZ
 sin(wx)的最小正周期为4p,则w=
sin(wx)的最小正周期为4p,则w=