题目内容
已知长方形ABCD,AB= ,BC=1.以AB的中点O为原点建立如图所示的平面直角坐标系xoy.椭圆Γ以A、B为焦点,且过C、D两点.
,BC=1.以AB的中点O为原点建立如图所示的平面直角坐标系xoy.椭圆Γ以A、B为焦点,且过C、D两点.(Ⅰ)求椭圆Γ的标准方程;
(Ⅱ)过点P(0,2)的直线l交椭圆Γ于M,N两点,是否存在直线l,使得OM⊥ON?若存在,求出直线l的方程;若不存在,说明理由.

【答案】分析:(1)由题意可得点A,B,C的坐标,设出椭圆的标准方程,根据题意知2a=AC+BC,求得a,进而根据b,a和c的关系求得b,则椭圆的方程可得.
(2)设直线l的方程为y=kx+2.与椭圆方程联立,根据判别式大于0求得k的范围,设M,N两点坐标分别为(x1,y1),(x2,y2).根据韦达定理求得x1+x2和x1x2,进而根据OM⊥ON,推断则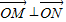 ,得知x1x2+y1y2=0,根据x1x2求得y1y2代入即可求得k,最后检验看是否符合题意.
,得知x1x2+y1y2=0,根据x1x2求得y1y2代入即可求得k,最后检验看是否符合题意.
解答:解:(1)由题意可得点A,B,C的坐标分别为(-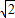 ,0),(
,0),(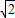 ,0),(
,0),(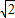 ,1)
,1)
设椭圆的标准方程是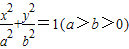 .
.
则2a=AC+BC,
即2a=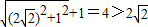 ,所以a=2.
,所以a=2.
所以b2=a2-c2=4-2=2.
所以椭圆的标准方程是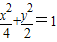 .
.
(2)由题意知,直线l的斜率存在,可设直线l的方程为y=kx+2.
由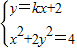 得(1+2k2)x2+8kx+4=0.
得(1+2k2)x2+8kx+4=0.
因为M,N在椭圆上,
所以△=64k2-16(1+2k2)>0.
设M,N两点坐标分别为(x1,y1),(x2,y2).
则x1+x2=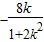 ,x1x2=
,x1x2=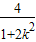 ,
,
由于OM⊥ON,则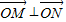 ,
,
所以x1x2+y1y2=0,
所以,x1x2+(kx1+2)(kx2+2)=0,
即(1+k2)x1x2+2k(x1+x2)+4=0,
所以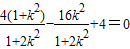 ,即
,即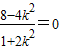 ,
,
得k2=2,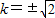
经验证,此时△=48>0.
所以直线l的方程为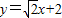 ,或
,或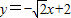 .
.
即所求直线存在,其方程为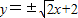 .
.
点评:本题主要考查了椭圆的标准方程以及直线与椭圆的关系.在设直线方程时一定要看斜率的存在情况,最后还要检验斜率k是否符合题意.
(2)设直线l的方程为y=kx+2.与椭圆方程联立,根据判别式大于0求得k的范围,设M,N两点坐标分别为(x1,y1),(x2,y2).根据韦达定理求得x1+x2和x1x2,进而根据OM⊥ON,推断则
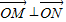 ,得知x1x2+y1y2=0,根据x1x2求得y1y2代入即可求得k,最后检验看是否符合题意.
,得知x1x2+y1y2=0,根据x1x2求得y1y2代入即可求得k,最后检验看是否符合题意.解答:解:(1)由题意可得点A,B,C的坐标分别为(-
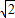 ,0),(
,0),(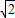 ,0),(
,0),(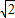 ,1)
,1)设椭圆的标准方程是
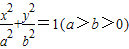 .
.则2a=AC+BC,
即2a=
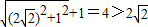 ,所以a=2.
,所以a=2.所以b2=a2-c2=4-2=2.
所以椭圆的标准方程是
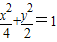 .
.(2)由题意知,直线l的斜率存在,可设直线l的方程为y=kx+2.
由
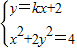 得(1+2k2)x2+8kx+4=0.
得(1+2k2)x2+8kx+4=0.因为M,N在椭圆上,
所以△=64k2-16(1+2k2)>0.
设M,N两点坐标分别为(x1,y1),(x2,y2).
则x1+x2=
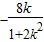 ,x1x2=
,x1x2=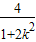 ,
,由于OM⊥ON,则
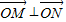 ,
,所以x1x2+y1y2=0,
所以,x1x2+(kx1+2)(kx2+2)=0,
即(1+k2)x1x2+2k(x1+x2)+4=0,
所以
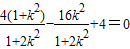 ,即
,即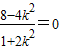 ,
,得k2=2,
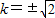
经验证,此时△=48>0.
所以直线l的方程为
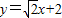 ,或
,或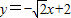 .
.即所求直线存在,其方程为
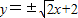 .
.点评:本题主要考查了椭圆的标准方程以及直线与椭圆的关系.在设直线方程时一定要看斜率的存在情况,最后还要检验斜率k是否符合题意.

练习册系列答案
相关题目
 已知长方形ABCD,AB=6,BC=7/4.以AB的中点0为原点建立如图所示的平面直角坐标系x0y
已知长方形ABCD,AB=6,BC=7/4.以AB的中点0为原点建立如图所示的平面直角坐标系x0y 如图,已知长方形ABCD的两条对角线的交点为E(1,0),且AB与BC所在的直线方程分别为:x+3y-5=0与ax-y+5=0.
如图,已知长方形ABCD的两条对角线的交点为E(1,0),且AB与BC所在的直线方程分别为:x+3y-5=0与ax-y+5=0.
 (2013•日照一模)已知长方形ABCD,AB=2
(2013•日照一模)已知长方形ABCD,AB=2