Question

【题目】已知为抛物线的焦点，为的准线与轴的交点，点在抛物线上，设，，，有以下个结论：

①的最大值是；②；③存在点，满足.

其中正确结论的序号是______.

Answer 1

【答案】①②③

【解析】

由直线与抛物线相切可求得的最大值，可判断命题①的正误；利用弦化切的思想和正弦定理边角互化思想可判断命题②的正误；由结合化简得出，判断该方程在时是否有根，由此可判断命题③的正误，综合可得出结论.

如下图所示：

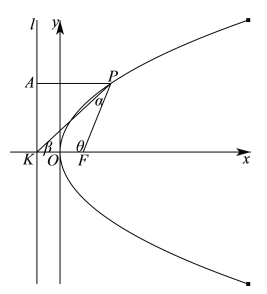
易知点，可设直线的方程为，

由图形可知，当直线与抛物线相切时，取最大值，

联立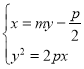，消去得，，得，

此时，直线的斜率为，所以，的最大值为，命题①正确；

过点作抛物线准线的垂线，垂足为点，则，

由抛物线的定义可知，则，

在中，由正弦定理得，所以，命题②正确；

若存在点，使得，则，可得，则.

由②知

即，

，则，

构造函数，则，，

由零点存在定理可知，函数在区间上有零点，

所以，关于的方程在时有实数解，命题③正确.

因此，正确结论的序号为①②③.

故答案为：①②③.