题目内容
设数列{an}前n项和为Sn,点 均在直线
均在直线 上.
上.
(1)求数列{an}的通项公式;
(2)设 ,Tn是数列{bn}的前n项和,试求Tn;
,Tn是数列{bn}的前n项和,试求Tn;
(3)设cn=anbn,Rn是数列{cn}的前n项和,试求Rn.
(1) (2)
(2) (3)
(3)
解析试题分析:(1)将点代入直线方程整理可得 ,用公式
,用公式 可推导出
可推导出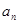 。(2)由
。(2)由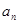 可得
可得 ,可证得数列
,可证得数列 为等比数列 ,用等比数列的前
为等比数列 ,用等比数列的前 项和公式可求其前
项和公式可求其前 项和
项和 。(3)因为
。(3)因为 等差
等差 等比,所以用错位相减法求数列
等比,所以用错位相减法求数列 的前
的前 项和。
项和。
试题解析:(1)依题意得,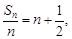 即
即 . (1分)
. (1分)
当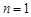 时,
时,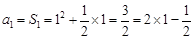 . (2分)
. (2分)
当 时,
时,  ; (4分)
; (4分)
所以 . (5分)
. (5分)
(2)由(1)得 , (6分)
, (6分)
由 , (7分)
, (7分)
由 ,可知{bn}为首项为9,公比为9的等比数列. (8分)
,可知{bn}为首项为9,公比为9的等比数列. (8分)
故 . (9分)
. (9分)
(3)由(1)、(2)得 (10分)
(10分)  (11分)
(11分) (12分)
(12分) (13分)
(13分) (14分)
(14分)
考点:1公式法求数列的通项公式;2等比数列的定义;3等比数列的前 项和;4错位相减法求数列的前
项和;4错位相减法求数列的前 项和。
项和。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 改选B菜;而选B菜的,下星期一会有
改选B菜;而选B菜的,下星期一会有 改选A菜。用
改选A菜。用 分别表示第
分别表示第 个星期选A的人数和选B的人数.
个星期选A的人数和选B的人数. 表示
表示 ,判断数列
,判断数列 是否成等比数列并说明理由;
是否成等比数列并说明理由;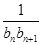 ,记数列{cn}的前n项和Tn.若对?n∈N*,Tn≤k(n+4)恒成立,求实数k的取值范围.
,记数列{cn}的前n项和Tn.若对?n∈N*,Tn≤k(n+4)恒成立,求实数k的取值范围. 满足
满足 , 且
, 且 ,其中
,其中 .
. 满足
满足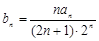 ,是否存在正整数
,是否存在正整数 ,使得
,使得 成等比数列?若存在,求出所有的
成等比数列?若存在,求出所有的 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。 ,记数列
,记数列 的前
的前 项和为
项和为 ,其中
,其中 。
。 中,
中,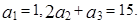
 通项公式;
通项公式; 满足
满足 ,求数列
,求数列 的前
的前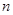 项和
项和 。
。 的首项
的首项 ,公差
,公差 .且
.且 分别是等比数列
分别是等比数列 的
的 .
.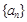 与
与 的通项公式;
的通项公式; 对任意自然数
对任意自然数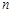 均有
均有
 成立,求
成立,求
 的值.
的值.