题目内容
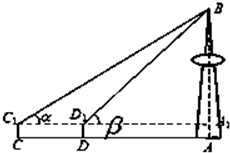如图所示，C、D、A三点在同一水平线上，AB是塔的中轴线，在C、D两处测得塔顶部B处的仰角分别是α和β，如果C、D间的距离是a，测角仪高为b，则塔高为（ ）分析：分别在△BCD、△ABD这两个三角形中运用正弦定理，即可求解．
解答：解：在△BCD中，
=
∴
=
即BD=
在△ABD中，
=
∴
=
即AB=BD•sinβ=
则塔高为
-b
故选：A
| CD |
| sin∠CBD |
| BD |
| sin∠C |
∴
| α |
| sin(β-α) |
| BD |
| sinα |
即BD=
| asinα |
| sin(β-α) |
在△ABD中，
| AB |
| sin∠ADB |
| BD |
| sin∠A |
∴
| AB |
| sinβ |
| BD |
| sin90° |
即AB=BD•sinβ=
| asinαsinβ |
| sin(β-α) |
则塔高为
| asinαsinβ |
| sin(β-α) |
故选：A
点评：此题考查了正弦定理的运用，灵活运用定理是解题的关键，属于中档题．
练习册系列答案
相关题目
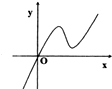定义在R上的函数f（x）满足f（4）=1，f′（x）为f（x）的导函数，已知y=f′（x）的图象如图所示，若两个正数a，b满足f(2a+b)＜1，则| b+1 |
| a+1 |
A、(
| ||||
B、(-∞，
| ||||
C、(
| ||||
| D、（-∞，3） |
（2011•广州模拟）已知正方形ABCD的边长为2，AC∩BD=O．将正方形ABCD沿对角线BD折起，使AC=a，得到三棱锥A-BCD，如图所示． 
（2005•海淀区二模）函数f（x）（x∈R）的图象如图所示，则当0＜a＜1时，函数g（x）=af（x）的单调减区间是（ ）