题目内容
 (2013•安徽)如图,四棱锥P-ABCD的底面ABCD是边长为2的菱形,∠BAD=60°,已知PB=PD=2,PA=
(2013•安徽)如图,四棱锥P-ABCD的底面ABCD是边长为2的菱形,∠BAD=60°,已知PB=PD=2,PA=| 6 |
(Ⅰ)证明:PC⊥BD
(Ⅱ)若E为PA的中点,求三棱锥P-BCE的体积.
分析:(I)连接AC交BD于O,连接PO.菱形ABCD中,证出AC⊥BD且O是BD的中点,从而得到PO是等腰△PBD中,PO是底边BD的中线,可得PO⊥BD,结合PO、AC是平面PAC内的相交直线,证出BD⊥平面PAC,从而得到PC⊥BD;
(II)根据ABCD是边长为2的菱形且∠BAD=60°,算出△ABC的面积为
,△PAO中证出AO2+PO2=6=PA2可得PO⊥AC,结合PO⊥BD证出PO⊥平面ABCD,所以PO=
是三棱锥P-ABC的高,从而三棱锥P-ABC的体积VP-ABC=1,再由E为PA中点算出三棱锥E-ABC的体积VE-ABC=
,进而可得三棱锥P-BCE的体积等于VP-ABC-VE-ABC=
,得到本题答案.
(II)根据ABCD是边长为2的菱形且∠BAD=60°,算出△ABC的面积为
| 3 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
解答: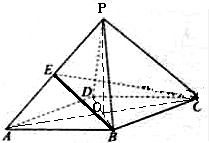 解:(I)连接AC交BD于O,连接PO
解:(I)连接AC交BD于O,连接PO
∵四边形ABCD是菱形,∴AC⊥BD,且O是BD的中点
∵△PBD中,PD=PB,O为BD中点,∴PO⊥BD
∵PO、AC?平面PAC,PO∩AC=O,∴BD⊥平面PAC,
∵PC?平面PAC,∴PC⊥BD;
(II)∵ABCD是边长为2的菱形,∠BAD=60°,
∴BO=
AB=1,AC=
AB=2
,可得△ABC的面积为S=
AC×BO=
∵△PBD中,PB=PD=BD=2,∴中线PO=
BD=
因此,△PAO中AO2+PO2=6=PA2
∴PO⊥AC,结合PO⊥BD得到PO⊥平面ABCD,
得到三棱锥P-ABC的体积VP-ABC=
×S△ABC×PO=
×
×
=1
∵E为PA中点,∴E到平面ABC的距离d=
PO=
由此可得三棱锥E-ABC的体积VE-ABC=
×S△ABC×d=
×
×
=
因此,三棱锥P-BCE的体积VP-EBC=VP-ABC-VE-ABC=
.
 解:(I)连接AC交BD于O,连接PO
解:(I)连接AC交BD于O,连接PO∵四边形ABCD是菱形,∴AC⊥BD,且O是BD的中点
∵△PBD中,PD=PB,O为BD中点,∴PO⊥BD
∵PO、AC?平面PAC,PO∩AC=O,∴BD⊥平面PAC,
∵PC?平面PAC,∴PC⊥BD;
(II)∵ABCD是边长为2的菱形,∠BAD=60°,
∴BO=
| 1 |
| 2 |
| 3 |
| 3 |
| 1 |
| 2 |
| 3 |
∵△PBD中,PB=PD=BD=2,∴中线PO=
| ||
| 2 |
| 3 |
因此,△PAO中AO2+PO2=6=PA2
∴PO⊥AC,结合PO⊥BD得到PO⊥平面ABCD,
得到三棱锥P-ABC的体积VP-ABC=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 3 |
∵E为PA中点,∴E到平面ABC的距离d=
| 1 |
| 2 |
| ||
| 2 |
由此可得三棱锥E-ABC的体积VE-ABC=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
因此,三棱锥P-BCE的体积VP-EBC=VP-ABC-VE-ABC=
| 1 |
| 2 |
点评:本题给出底面为菱形的四棱锥,求证线线垂直并求锥体的体积,着重考查了线面垂直的判定与性质、菱形的性质及面积计算和锥体体积公式等知识,属于中档题.

练习册系列答案
相关题目
 (2013•安徽)如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S,则下列命题正确的是
(2013•安徽)如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S,则下列命题正确的是 (2013•安徽)如图所示,程序框图(算法流程图)的输出结果中( )
(2013•安徽)如图所示,程序框图(算法流程图)的输出结果中( ) (2013•安徽)如图所示,程序据图(算法流程图)的输出结果为( )
(2013•安徽)如图所示,程序据图(算法流程图)的输出结果为( )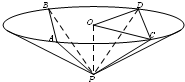 (2013•安徽)如图,圆锥顶点为P,底面圆心为O,其母线与底面所成的角为22.5°,AB和CD是底面圆O上的两条平行的弦,轴OP与平面PCD所成的角为60°,
(2013•安徽)如图,圆锥顶点为P,底面圆心为O,其母线与底面所成的角为22.5°,AB和CD是底面圆O上的两条平行的弦,轴OP与平面PCD所成的角为60°,