题目内容
已知E、F分别是棱长为a的正方体ABCD—A1B1C1D1的棱A1A、CC1的中点,求四棱锥C1—B1EDF的体积.
解法一:连结A1C1、B1D1交于O1,过O1作O1H⊥B1D于H,
∵EF∥A1C1,
∴A1C1∥平面B1EDF.
∴C1到平面B1EDF的距离就是A1C1到平面B1EDF的距离.
∵平面B1D1D⊥平面B1EDF,
∴O1H⊥平面B1EDF,即O1H为棱锥的高.
∵△B1O1H∽△B1DD1,
∴O1H=![]() =
=![]() a,
a,
![]() =
=![]()
![]() ·O1H=
·O1H=![]() ·
·![]() ·EF·B1D·O1H=
·EF·B1D·O1H=![]() ·
·![]() ·
·![]() a·
a·![]() a·
a·![]() a=
a=![]() a3.
a3.
解法二:连结EF,设B1到平面C1EF的距离为h1,D到平面C1EF的距离为h2,则h1+h2=B1D1=![]() a,
a,
∴![]() =
=![]() +
+![]() =
=![]() ·
·![]() ·(h1+h2)=
·(h1+h2)=![]() a3.
a3.
解法三:![]() =
=![]() -
-![]() -
-![]() =
=![]() a3.
a3.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
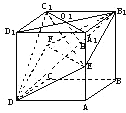 已知E、F分别是棱长为a的正方体ABCD-A1B1C1D1的棱A1A、CC1的中点,求四棱锥C1-B1EDF的体积.
已知E、F分别是棱长为a的正方体ABCD-A1B1C1D1的棱A1A、CC1的中点,求四棱锥C1-B1EDF的体积.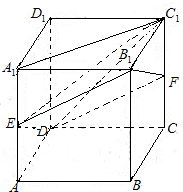 如图,已知E、F分别是棱长为a的正方体ABCD-A1B1C1D1的棱AA1、CC1的中点
如图,已知E、F分别是棱长为a的正方体ABCD-A1B1C1D1的棱AA1、CC1的中点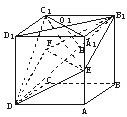 已知E、F分别是棱长为a的正方体ABCD-A1B1C1D1的棱A1A、CC1的中点,求四棱锥C1-B1EDF的体积.
已知E、F分别是棱长为a的正方体ABCD-A1B1C1D1的棱A1A、CC1的中点,求四棱锥C1-B1EDF的体积.
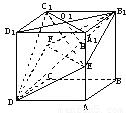 已知E、F分别是棱长为a的正方体ABCD-A1B1C1D1的棱A1A、CC1的中点,求四棱锥C1-B1EDF的体积.
已知E、F分别是棱长为a的正方体ABCD-A1B1C1D1的棱A1A、CC1的中点,求四棱锥C1-B1EDF的体积.