题目内容
已知等差数列首项为2，末项为62，公差为4，则这个数列共有
- A.13项
- B.14项
- C.15项
- D.16项
D
分析：由等差数列首项为2，末项为62，公差为4，得62=2+（n-1）×4，由此能求出这个数列有多少项．
解答：∵等差数列首项为2，末项为62，公差为4，
∴62=2+（n-1）×4，
解得n=16．
所以这个数列有16项．
故选D．
点评：本题考查等差数列的通项公式的应用，是基础题．解题时要认真审题，仔细解答．
分析：由等差数列首项为2，末项为62，公差为4，得62=2+（n-1）×4，由此能求出这个数列有多少项．
解答：∵等差数列首项为2，末项为62，公差为4，
∴62=2+（n-1）×4，
解得n=16．
所以这个数列有16项．
故选D．
点评：本题考查等差数列的通项公式的应用，是基础题．解题时要认真审题，仔细解答．
练习册系列答案
能考试期末冲刺卷系列答案
相关题目
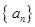的任意连续三项均能构成一个三角形的三边长，则称
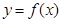使得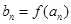
仍为一个“三角形”数列，则称
.
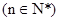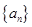是首项为2，公差为1的等差数列，若
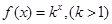是数列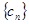
的首项为2010，
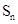是数列
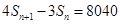，证明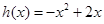
，
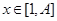，和数列1，
，
，（
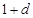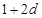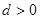）提出一个正确的命题，并说明理由．