Question

若不等式|x+2|+|x-3|＜a的解集不是空集,求a的取值范围.

Answer 1

解法一:|x+2|+|x-3|表示数轴上的点x到点-2和3的距离之和,其最小值为5,因此,若不等式|x+2|+|x-3|＜a的解集不是空集,则只需a＞5.

解法二:令y=|x+2|+|x-3|,

当x≤-2时,y=-x-2-x+3=-2x+1;

当-2＜x＜3时,y=x+2-x+3=5;

当x≥3时,y=x+2+x-3=2x-1,

即y=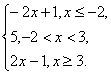

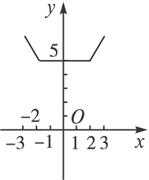
以上的函数图象如上图所示.

要使y＜a的解集不空,只需a＞5即可.