题目内容
如图所示,曲线段OMB是函数f(x)=x2(0＜x＜6)的图象,BA⊥x轴于点A,曲线段OMB上一点M(t,f(t))处的切线PQ交x轴于点P,交线段AB于点Q.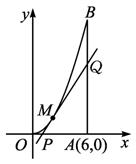
(1)试用t表示切线PQ的方程;
(2)设△QAP的面积为g(t);若函数g(t)在(m,n)上单调递减,试求出m的最小值;
(3)试求g(t)的取值范围.
解：(1)设点M(t,t2),又f′(x)=2x,
∴过点M的切线PQ的斜率k=2t.
∴切线PQ的方程为y=2tx-t2.
(2)由(1)可求得P(
,0)、Q(6,12t-t2),
∴g(t)=S△QAP=
(6-
t)(12t-t2)=
-6t2+36t.
由于g′(t)=
-12t+36,
令g′(t)＜0,则4＜t＜12,考虑到0＜t＜6,
∴4＜t＜6.
∴函数g(t)的单调递减区间是(4,6).
因此m的最小值为4.
(3)由(2)知,g(t)在区间(4,6)上递减,
∴此时S△QAP∈(g(6),g(4))=(54,64).
令g′(t)＞0,则0＜t＜4,
∴g(t)在区间(0,4)上递增.
∴S△QAP∈(g(0),g(4))=(0,64).
又g(4)=64,
故g(t)的值域为(0,64］.
练习册系列答案
相关题目
9、设函数y=f（x）是最小正周期为2的偶函数，它在区间[0，1]上的图象为如图所示的线段AB，则在区间[1，2]上f（x）=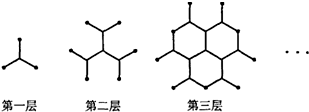
（2013•宁德模拟）一种平面分形图的形成过程如图所示，第一层是同 一点出发的三条线段，长度均为1，每两条线段夹角为 120°；第二层是在第一层的每一条线段末端，再生成 两条与该线段成120°角的线段，长度不变；第三层按 第二层的方法再在第二层每一条线段的末端各生成两条 线段；重复前面的作法，直至第6层，则分形图第6层 各条线段末端之间的距离的最大值为