题目内容
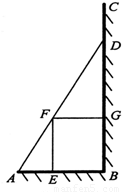
 如图,某园林绿化单位准备在一直角ABC内的空地上植造一块“绿地△ABD”,规划在△ABD的内接正方形BEFG内种花,其余地方种草,若AB=a,∠DAB=θ,种草的面积为S1,种花的面积为S2,比值
如图,某园林绿化单位准备在一直角ABC内的空地上植造一块“绿地△ABD”,规划在△ABD的内接正方形BEFG内种花,其余地方种草,若AB=a,∠DAB=θ,种草的面积为S1,种花的面积为S2,比值| S1 | S2 |
(I)试用a,θ表示S1,S2;
(II)若a为定值,BC>AB.当θ为何值时,“规划和谐度”有最小值?最小值是多少?
分析:(I)求出△ABD的面积为,设正方形BEFG的边长为t,利用三角形的相似求出S2,然后求出S1
(II)由(I)
,通过tanθ∈(0,+∞),通过基本不等式推出,当θ=
时,
有最小值1.
(II)由(I)
| S1 |
| S2 |
| π |
| 4 |
| S1 |
| S2 |
解答:解:(I)∵BD=atanθ,
∴△ABD的面积为
a2tanθ(θ∈(0,
))…(2分)
设正方形BEFG的边长为t,
则由
=
,得
=
,解得t=
,…(4分)
∴S2=
,
∴S1=
a2tanθ-S2=
a2tanθ-
.…(6分)
(II)由(I)
=
-1,…(8分)
∵tanθ∈(0,+∞),
∴
=
(tanθ+
+2)-1=
(tanθ+
)≥1,…(10分)
当且仅当tanθ=1时取等号,此时θ=
.
∴当θ=
时,
有最小值1.…(12分)
∴△ABD的面积为
| 1 |
| 2 |
| π |
| 2 |
设正方形BEFG的边长为t,
则由
| FG |
| AB |
| DG |
| DB |
| t |
| a |
| atanθ-t |
| atanθ |
| atanθ |
| 1+tanθ |
∴S2=
| a2tan2θ |
| (1+tanθ)2 |
∴S1=
| 1 |
| 2 |
| 1 |
| 2 |
| a2tan2θ |
| (1+tanθ)2 |
(II)由(I)
| S1 |
| S2 |
| (1+tanθ)2 |
| 2tanθ |
∵tanθ∈(0,+∞),
∴
| S1 |
| S2 |
| 1 |
| 2 |
| 1 |
| tanθ |
| 1 |
| 2 |
| 1 |
| tanθ |
当且仅当tanθ=1时取等号,此时θ=
| π |
| 4 |
∴当θ=
| π |
| 4 |
| S1 |
| S2 |
点评:本题考查解三角形的实际应用,基本不等式的应用,考查计算能力.

练习册系列答案
相关题目
 ,种草的面积为
,种草的面积为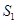 ,种花的面积为
,种花的面积为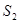 ,比值
,比值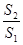 称为“规划和谐度”。
称为“规划和谐度”。 表示
表示 为定值,BC >AB。当
为定值,BC >AB。当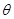 为何值时,“规划和谐度”有最小值?最小值是多少?
为何值时,“规划和谐度”有最小值?最小值是多少?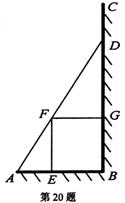
 如图,某园林绿化单位准备在一直角ABC内的空地上植造一块“绿地△ABD”,规划在△ABD的内接正方形BEFG内种花,其余地方种草,若AB=a,∠DAB=θ,种草的面积为S1,种花的面积为S2,比值
如图,某园林绿化单位准备在一直角ABC内的空地上植造一块“绿地△ABD”,规划在△ABD的内接正方形BEFG内种花,其余地方种草,若AB=a,∠DAB=θ,种草的面积为S1,种花的面积为S2,比值 称为“规划和谐度”.
称为“规划和谐度”.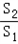 称为“规划和谐度”.
称为“规划和谐度”.
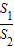 称为“规划和谐度”.
称为“规划和谐度”.