题目内容
直角三角形ABC中,∠C=90°,∠A=30°,AC=2
,BC=2,CD为斜边AB边上的高,将三角形ACD沿CD折起与面BCD成60°的二面角,则翻折后线段AB的长为
.
| 3 |
| 7 |
| 7 |
分析:直角三角形ABC中,由∠C=90°,∠A=30°,AC=2
,BC=2,CD为斜边AB边上的高,得到AB=4,CD=
,BD=1,AD=3.将三角形ACD沿CD折起与面BCD成60°的二面角,由CD⊥AD,CD⊥BD,知∠ADB=60°,由AD=3,BD=1,利用余弦定理能求出AB的长.
| 3 |
| 3 |
解答:解:如图,直角三角形ABC中,
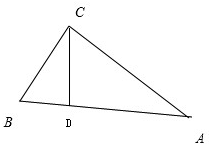
∵∠C=90°,∠A=30°,AC=2
,BC=2,CD为斜边AB边上的高,
∴AB=
=4,
∴CD=
=
,
∴BD=
=1,AD=4-1=3,
如图,将三角形ACD沿CD折起与面BCD成60°的二面角,
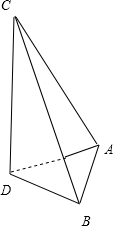
∵CD⊥AD,CD⊥BD,∴∠ADB=60°,
∵AD=3,BD=1,
∴由余弦定理,得:AB=
=
.
故答案为:
.

∵∠C=90°,∠A=30°,AC=2
| 3 |
∴AB=
| 4+12 |
∴CD=
2×2
| ||
| 4 |
| 3 |
∴BD=
22-(
|
如图,将三角形ACD沿CD折起与面BCD成60°的二面角,

∵CD⊥AD,CD⊥BD,∴∠ADB=60°,
∵AD=3,BD=1,
∴由余弦定理,得:AB=
| 9+1-2×3×1×cos60° |
| 7 |
故答案为:
| 7 |
点评:本题考查空间中两点间距离的求法,解题时要认真审题,仔细解答,注意二面角和余弦定理的合理运用.

练习册系列答案
相关题目
 15、(选做题)(几何证明选讲选做题)如图,直角三角形ABC中,∠B=90°,AB=4,以BC为直径的圆交AC边于点D,AD=2,则∠C的大小为
15、(选做题)(几何证明选讲选做题)如图,直角三角形ABC中,∠B=90°,AB=4,以BC为直径的圆交AC边于点D,AD=2,则∠C的大小为 (2012•宝鸡模拟)如图,已知PA⊥平面ABC,且
(2012•宝鸡模拟)如图,已知PA⊥平面ABC,且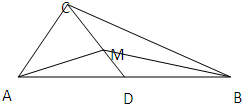 如图:直角三角形ABC中,AC⊥BC,AB=2,D是AB的中点,M是CD上的动点.
如图:直角三角形ABC中,AC⊥BC,AB=2,D是AB的中点,M是CD上的动点.