题目内容
如右图所示,一座圆拱桥,当水面在图位置甲时,拱顶离水面2 m,水面宽 12 m,当水面下降1 m后,水面宽多少米?

甲
水面下降1米后,水面宽为![]()
解析:
以圆拱拱顶为坐标原点,以过拱顶的竖直直线为y轴,建立直角坐标系,设圆心为C,水面所在弦的端点为A、B,则由已知得A(6,-2).
设圆的半径为r,则C(0,-r),即圆的方程为
x2+(y+r)2=r2.①
将点A的坐标为(6,-2)代入方程①,解得r=10.

乙∴圆的方程为x2+(y+10)2=100.②
当水面下降1米后,可设点A′的坐标为(x0,-3)(x0>3),如图乙所示,将A′的坐标(x0,-3)代入方程②,求得![]() .
.
∴水面下降1米后,水面宽为
![]() .
.

练习册系列答案
相关题目


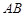 的长为
的长为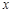 ,
, 表示弧
表示弧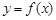 的图象是(
)
的图象是(
) 
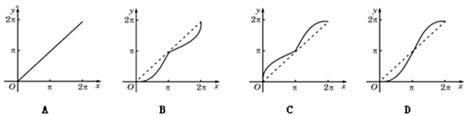
 是圆
是圆 上的三点,
上的三点, 的延长线与线段
的延长线与线段 交于圆内一点
交于圆内一点 ,若
,若 ,则
,则 B.
B. C.
C. D.
D.
