题目内容
已知函数f(x)=ax3+(1)证明0<a≤3;
(2)求b的取值范围;
(3)若函数h(x)=f′(x)
解:设f′(x)=3ax2+2![]() x-a2=
x-a2=
∴x1+x2=-![]() ,x1x2=-
,x1x2=-![]() .?
.?
由a>0,得x1<0<x2.?
∵|x1|+|x2|=2,?
∴x2-x1=2.?
(1)证明:∵-x1和x2是方程T2-2T+![]() =0的两个实根,?
=0的两个实根,?
∵方程有解,∴Δ=4-![]() ≥0,?
≥0,?
得0<a≤3. ?
(2)由(x1+x2)2-4x1x2=4,?
得![]() +
+![]() =4.?
=4.?
∴b=
∴b′=-
由b′=0,得a=0或a=2,?
∵0<a≤3,?
∴0<a≤2时,b′≥0,b在(0,2]上单调递增;?
2≤a≤3时,b′≤0,b在[2,3]上单调递减.?
∴a=2时,b取最大值12,?
a=3时,b=0,?
a=0时,b=0. ?
∴0≤b≤12.?
(也可用下面方法?
∴b=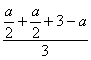 )3=12.?
)3=12.?
∴0≤b≤12)?
(3)证明:h(x)=
=
其图象是开口向上的抛物线.?
∵x1<x<2且x1<x2,x2-x1=2,?
对称轴为x=![]() =
=![]() =x2.?
=x2.?
由x1<x<2,?
若x2≤2,则0=h(x1)>h(x)≥h(x)=
∴|h(x)|≤
若2<x2,则0=h(x1)>h(x)>h(2)>h(x2)=-
∴|h(x)|<
由0<a≤3,综上,得|h(x)|≤

| 1 |
| 2x+1 |
A、
| ||
| B、2 | ||
C、
| ||
| D、3 |