题目内容
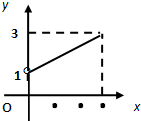已知函数f（x）是定义在[-3，0）∪（0，3]上的奇函数，当x＞0时f（x）的图象如图所示，那么f（x）的值域是分析：根据函数奇偶性的性质，确定函数的值域即可．
解答：解：∵当0＜x≤3时，函数单调递增，由图象知1＜f（x）≤3，
当-3≤x＜0时，在0＜-x≤3，即此时函数也单调递增，
且1＜f（-x）≤3，
∵函数是奇函数，
∴f（-x）=-f（x），
∴1＜-f（x）≤3，
即-3≤f（x）＜-1，
∴f（x）的值域是[-3，-1）∪（1，3]，
故答案为：[-3，-1）∪（1，3]．
当-3≤x＜0时，在0＜-x≤3，即此时函数也单调递增，
且1＜f（-x）≤3，
∵函数是奇函数，
∴f（-x）=-f（x），
∴1＜-f（x）≤3，
即-3≤f（x）＜-1，
∴f（x）的值域是[-3，-1）∪（1，3]，
故答案为：[-3，-1）∪（1，3]．
点评：本题主要考查函数值域的求法，利用函数奇偶性的性质进行转化是解决本题的关键．
练习册系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
相关题目
已知函数f（x）=x+