题目内容

已知正方体ABCD-A1B1C1D1内有一个内切球O，则在正方体ABCD-A1B1C1D1内任取点M，点M在球O内的概率是

A.
$数学公式$
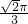
B.
$数学公式$
C.
$数学公式$
D.
$数学公式$

C
分析：本题是几何概型问题，欲求点M在球O内的概率，先由正方体ABCD-A1B1C1D1内的内切球O，求出其体积，再根据几何概型概率公式结合正方体的体积的方法易求解．
解答：

解：本题是几何概型问题，设正方体的棱长为：2．
正方体ABCD-A1B1C1D1内的内切球O的半径是其棱长的一增，
其体积为：V₁= $\text{[math]}$
则点M在球O内的概率是 $\text{[math]}$ = $\text{[math]}$ ．
故选C．
点评：本小题主要考查几何概型、几何概型的应用、几何体和体积等基础知识，考查空间想象能力、化归与转化思想．属于基础题．

练习册系列答案

走进新课程课课练系列答案

百校联盟金考卷系列答案

步步高学案导学与随堂笔记系列答案

诚成教育学业评价系列答案

创新课时精练系列答案

创新设计课堂讲义系列答案

创新优化新天地试卷系列答案

高中得分王系列答案

激活思维智能优选卷系列答案

金榜名卷复习冲刺卷系列答案

相关题目

如图，已知正方体ABCD-A₁B₁C₁D₁的棱长为2，点P在平面DD₁C₁C内，PD₁=PC₁=

．求证：
（1）平面PD₁A₁⊥平面D₁A₁BC；
（2）PC₁∥平面A₁BD．

已知正方体ABCD-A₁B₁C₁D₁中，E、F分别为BB₁、CC₁的中点，那么直线AE与D₁F所成角的余弦值为（　　）

已知正方体ABCD-A₁B₁C₁D₁中，E为棱CC₁的动点．
（1）当E恰为棱CC₁的中点时，试证明：平面A₁BD⊥平面EBD；
（2）在棱CC₁上是否存在一个点E，可以使二面角A₁-BD-E的大小为45°？如果存在，试确定点E在棱CC₁上的位置；如果不存在，请说明理由．

已知正方体ABCD-A₁B₁C₁D₁，则四面体A₁-C₁BD在面A₁B₁C₁D₁上的正投影的面积与该四面体表面积之比是

已知正方体ABCD-A₁B₁C₁D₁，O是底ABCD对角线的交点．
（1）求证：C₁O∥面AB₁D₁；
（2）求异面直线AD₁与 C₁O所成角的大小．