题目内容
抛物线y=ax2+bx+c(a≠0)的顶点满足下述三个条件:①在第三象限;②在直线y=x上;③到原点距离为2
思路解析:若建立一般式y=ax2+bx+c(a≠0)由题设条件将得到一个三元二次的方程组,解此三元二次方程需花较多时间,若建立顶点式y=a(x-h)2+h.顶点(h,h),h<0,则![]() ,∴h=-2.∴抛物线为y=a(x-2)2-2.最后利用|x1-x2|=8,求得a值.由抛物线的顶点(-2,-2)及对称轴方程x=-2,则可知抛物线与x轴的两交点到对称轴的距离都是4,∴抛物线与x轴的两交点坐标为(-6,0)与(2,0),从而建立抛物线与x轴交点的坐标式(也称标根式)最简.
,∴h=-2.∴抛物线为y=a(x-2)2-2.最后利用|x1-x2|=8,求得a值.由抛物线的顶点(-2,-2)及对称轴方程x=-2,则可知抛物线与x轴的两交点到对称轴的距离都是4,∴抛物线与x轴的两交点坐标为(-6,0)与(2,0),从而建立抛物线与x轴交点的坐标式(也称标根式)最简.
解:设抛物线的顶点为(h,h),且h<0,则![]()
![]() h=-2.
h=-2.
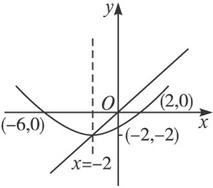
∴抛物线顶点为(-2,-2),抛物线的对称轴方程为x=-2.
∵抛物线被x轴截得的线段长为8,∴抛物线与x轴的两交点为(-6,0)、(2,0).
设抛物线为y=a(x+6)(x-2)(a≠0)过点(-2,-2),∴-2=a·4(-4)![]() a=
a=![]() .
.
∴抛物线的解析式为y=![]() (x+6) (x-2)=
(x+6) (x-2)= ![]() x2+
x2+![]() x-
x-![]() .
.

练习册系列答案
相关题目
抛物线y=ax2与直线y=kx+b(k≠0)交于A,B两点,且此两点的横坐标分别为x1,x2,直线与x轴的交点的横坐标是x3,则恒有( )
| A、x3=x1+x2 | B、x1x2=x1x3+x2x3 | C、x3+x1+x2=0 | D、x1x2+x1x3+x2x3=0 |
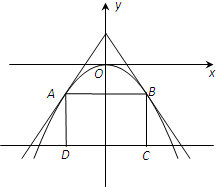 如图,过点(0,a3)(0<a<2)的两直线与抛物线y=-ax2相切于A,B两点,AD,BC垂直于直线y=-8,垂足分别为D、C,求矩形ABCD面积的最大值.
如图,过点(0,a3)(0<a<2)的两直线与抛物线y=-ax2相切于A,B两点,AD,BC垂直于直线y=-8,垂足分别为D、C,求矩形ABCD面积的最大值.