题目内容
已知最小正周期为2的函数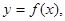 当
当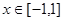 时,
时,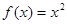 ,则函数
,则函数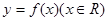 的图象与
的图象与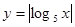 的图象的交点个数为
的图象的交点个数为
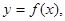 当
当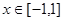 时,
时,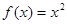 ,则函数
,则函数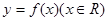 的图象与
的图象与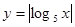 的图象的交点个数为
的图象的交点个数为 5
试题分析:做出函数
 ,
, 的图像,观察图像可知两函数有5个交点
的图像,观察图像可知两函数有5个交点
点评:数形结合法是高中数学常用的方法,在求解关于方程的根的个数,函数零点,图像交点问题时简单好用,其关键是准确的画出函数图象

练习册系列答案
相关题目
题目内容
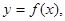 当
当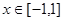 时,
时,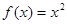 ,则函数
,则函数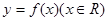 的图象与
的图象与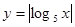 的图象的交点个数为
的图象的交点个数为  ,
, 的图像,观察图像可知两函数有5个交点
的图像,观察图像可知两函数有5个交点
