题目内容
已知f(x)=| x-2m-5 |
| x+2 |
| 7 |
| 2 |
(I)讨论f(x)在区间(-2,+∞)上的单调性,并证明;
(II)若方程f(x)=g(x)至少有一个正数根,求实数m的取值范围.
分析:(I)运用函数的定义判断证明函数的单调性的步骤:①取值x1,x2∈(-2,+∞);②作差f(x1)-f(x2)变形;③定号;④下结论;
(II)由f(x)=g(x),整理得:mx2+(m-3)x+1=0,然后对m进行分类讨论,研究方程f(x)=g(x)至少有一个正数根,从而求出实数m的取值范围.
(II)由f(x)=g(x),整理得:mx2+(m-3)x+1=0,然后对m进行分类讨论,研究方程f(x)=g(x)至少有一个正数根,从而求出实数m的取值范围.
解答:解:(I)因为f(x)=1-
,所以,当m>-
时,
f(x)在区间(-2,+∞)上为增函数,当m<-
时,f(x)在区间(-2,+∞)上为减函数.…(2分)
任取x1,x2∈(-2,+∞),且x1<x2,则f(x1)-f(x2)=-
+
=
,
因为x1,x2∈(-2,+∞),且x1<x2,
所以,(x1+2)(x2+2)>0,且x1-x2<0,当m>-
时,有f(x1)-f(x1)<0,f(x)在区间(-2,+∞)上为增函数;
当m<-
时,有f(x1)-f(x1)>0,f(x)在区间(-2,+∞)上为减函数.…(5分)
(II)f(x)=g(x)?x-2m-5=mx2+(m-2)x-2m-4
整理得:mx2+(m-3)x+1=0,…(5分),
令h(x)=mx2+(m-3)x+1
当m=0时,x=
,符合题设;…(6分)
当m<0时,必有△>0,且x1x2=
<0,h(-2)=2m+7≠0,符合题设;…(7分)
当m>0时,因为x1x2=
>0,所以,方程的两根必须都是正根,有:
,
解得:0<m≤1,
综上所述,m≤1且m≠-
.…(10分)
| 2m+7 |
| x+2 |
| 7 |
| 2 |
f(x)在区间(-2,+∞)上为增函数,当m<-
| 7 |
| 2 |
任取x1,x2∈(-2,+∞),且x1<x2,则f(x1)-f(x2)=-
| 2m+7 |
| x1+2 |
| 2m+7 |
| x2+2 |
| (2m+7)(x1-x2) |
| (x1+2)(x2+2) |
因为x1,x2∈(-2,+∞),且x1<x2,
所以,(x1+2)(x2+2)>0,且x1-x2<0,当m>-
| 7 |
| 2 |
当m<-
| 7 |
| 2 |
(II)f(x)=g(x)?x-2m-5=mx2+(m-2)x-2m-4
整理得:mx2+(m-3)x+1=0,…(5分),
令h(x)=mx2+(m-3)x+1
当m=0时,x=
| 1 |
| 3 |
当m<0时,必有△>0,且x1x2=
| 1 |
| m |
当m>0时,因为x1x2=
| 1 |
| m |
|
解得:0<m≤1,
综上所述,m≤1且m≠-
| 7 |
| 2 |
点评:本题主要考查函数单调性的应用.运用函数的定义判断证明函数的单调性的步骤:(1)取值;(2)作差变形;(3)定号;(4)下结论.取值时,必须注意定义中的x1、x2具有的三个特征;变形时,一定要分解完全,对于抽象函数问题注意合理的利用条件等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知f(x)=sin(x+
),g(x)=cos(x-
),则下列结论中正确的是( )
| π |
| 2 |
| π |
| 2 |
| A、函数y=f(x)•g(x)的最大值为1 | ||||
B、函数y=f(x)•g(x)的对称中心是(
| ||||
C、当x∈[-
| ||||
D、将f(x)的图象向右平移
|
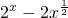 ,又a是函数g (x)=
,又a是函数g (x)=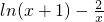 的正零点,则f(-2),f(a),f(1.5)的大上关系是
的正零点,则f(-2),f(a),f(1.5)的大上关系是