题目内容
x是实数,则下列不等式恒成立的是
- A.x2+4>4x
- B.

- C.lg(x2+1)>lg(2x)
- D.x2+1>x
D
分析:由于 x2-4x+4=(x-2)2≥0,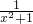 ≤1,lg(x2+1)≥lg(2x),故A、B、C不恒成立.由于x2-x+1=
≤1,lg(x2+1)≥lg(2x),故A、B、C不恒成立.由于x2-x+1= +
+ >0,故 x2+1>x 恒成立,由此得出结论.
>0,故 x2+1>x 恒成立,由此得出结论.
解答:由于 x2-4x+4=(x-2)2≥0,故A不恒成立.
由于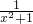 ≤1,故B不恒成立.
≤1,故B不恒成立.
由于 x2+1≥2x,故 lg(x2+1)≥lg(2x),故C不恒成立.
由于x2-x+1= +
+ >0,故 x2+1>x 恒成立,
>0,故 x2+1>x 恒成立,
故选D.
点评:本题主要考查不等式与不等关系,属于基础题.
分析:由于 x2-4x+4=(x-2)2≥0,
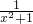 ≤1,lg(x2+1)≥lg(2x),故A、B、C不恒成立.由于x2-x+1=
≤1,lg(x2+1)≥lg(2x),故A、B、C不恒成立.由于x2-x+1= +
+ >0,故 x2+1>x 恒成立,由此得出结论.
>0,故 x2+1>x 恒成立,由此得出结论.解答:由于 x2-4x+4=(x-2)2≥0,故A不恒成立.
由于
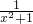 ≤1,故B不恒成立.
≤1,故B不恒成立.由于 x2+1≥2x,故 lg(x2+1)≥lg(2x),故C不恒成立.
由于x2-x+1=
 +
+ >0,故 x2+1>x 恒成立,
>0,故 x2+1>x 恒成立,故选D.
点评:本题主要考查不等式与不等关系,属于基础题.

练习册系列答案
相关题目
已知函数f(x)=
(x∈R)时,则下列结论不正确的是( )
| x |
| 1+|x| |
| A、?x∈R,等式f(-x)+f(x)=0恒成立 |
| B、?m∈(0,1),使得方程|f(x)|=m有两个不等实数根 |
| C、?x1,x2∈R,若x1≠x2,则一定有f(x1)≠f(x2) |
| D、?k∈(1,+∞),使得函数g(x)=f(x)-kx在R上有三个零点 |