题目内容
如图，四棱锥P—ABCD的底面是矩形，PA⊥平面ABCD，E、F分别是AB、PD的中点，又二面角PCDB为45°，求证：AF∥平面PEC.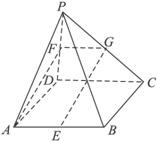
证明：取PC的中点G，连结EG、FG.∵F是PD的中点，
∴FG∥CD，且FG=
CD.
而AE∥CD，且AE=
CD,
∴EA∥GF，且EA=GF.
故四边形EGFA是平行四边形，从而EG∥AF.
又AF
平面PEC，EG
平面PEC，
∴AF∥平面PEC.
练习册系列答案
相关题目
题目内容
如图，四棱锥P—ABCD的底面是矩形，PA⊥平面ABCD，E、F分别是AB、PD的中点，又二面角PCDB为45°，求证：AF∥平面PEC.
证明：取PC的中点G，连结EG、FG.∵F是PD的中点，
∴FG∥CD，且FG=CD.
而AE∥CD，且AE=CD,
∴EA∥GF，且EA=GF.
故四边形EGFA是平行四边形，从而EG∥AF.
又AF平面PEC，EG平面PEC，
∴AF∥平面PEC.
如图，四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC=60°，PA=AB=BC，
如图，四棱锥P-ABCD中，底面ABCD是直角梯形，AB∥CD，∠DAB=60°，AB=AD=2CD=2，侧面PAD⊥底面ABCD，且△PAD为等腰直角三角形，∠APD=90°，M为AP的中点．
如图，四棱锥P-ABCD的底面ABCD是矩形，AB=2，
如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥底面ABCD，且PA=AB=1，
如图，四棱锥P-ABCD，PA⊥平面ABCD，ABCD是直角梯形，DA⊥AB，CB⊥AB，PA=2AD=BC=2，AB=