题目内容
双曲线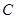 的中心在原点,右焦点为
的中心在原点,右焦点为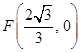 ,渐近线方程为
,渐近线方程为 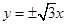 .
.
(1)求双曲线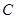 的方程;
的方程;
(2)设直线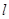 :
: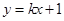 与双曲线
与双曲线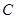 交于
交于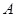 、
、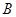 两点,问:当
两点,问:当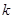 为何值时,以
为何值时,以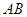 为直径的圆过原点;
为直径的圆过原点;
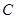 的中心在原点,右焦点为
的中心在原点,右焦点为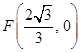 ,渐近线方程为
,渐近线方程为 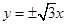 .
.(1)求双曲线
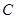 的方程;
的方程;(2)设直线
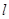 :
: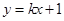 与双曲线
与双曲线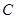 交于
交于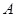 、
、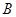 两点,问:当
两点,问:当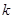 为何值时,以
为何值时,以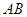 为直径的圆过原点;
为直径的圆过原点;(1)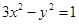 ;(2)
;(2)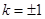
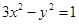 ;(2)
;(2)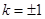
试题分析:(1)根据双曲线的几何性质可得:c=
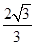 ,
,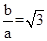 ,解方程组即可;(2)可以联立直线方程与双曲线方程,消去y得关于x的一元二次方程,利用韦达定理,结合以
,解方程组即可;(2)可以联立直线方程与双曲线方程,消去y得关于x的一元二次方程,利用韦达定理,结合以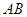 为直径的圆过原点时
为直径的圆过原点时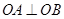 ,建立方程,即可解除k.
,建立方程,即可解除k.试题解析:(1)易知 双曲线的方程是
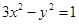 .
.(2)① 由
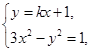 得
得 ,
,由
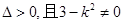 ,得
,得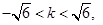 且
且 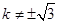 .
.设
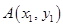 、
、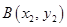 ,因为以
,因为以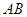 为直径的圆过原点,所以
为直径的圆过原点,所以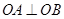 ,
,所以
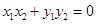 .又
.又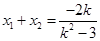 ,
,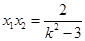 ,
,所以
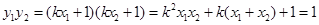 ,
,所以
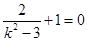 ,解得
,解得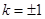 .
. 
练习册系列答案
相关题目
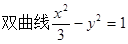 的右焦点到直线
的右焦点到直线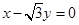 的距离是( )
的距离是( )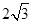
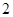
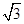
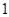
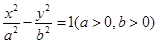 的焦点和虚轴端点,若线段FB的中点在双曲线C上,则双曲线C的离心率是___________.
的焦点和虚轴端点,若线段FB的中点在双曲线C上,则双曲线C的离心率是___________.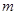 ,直线
,直线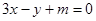 与双曲线
与双曲线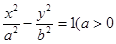 ,
,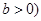 最多有一个交点,则双曲线的离心率等于( )
最多有一个交点,则双曲线的离心率等于( )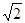
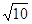
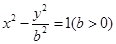 的一条渐近线的方程为
的一条渐近线的方程为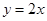 ,则
,则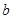 =_____ __.
=_____ __.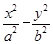 =1(a>0,b>0)的一个焦点,并与双曲线实轴垂直,已知拋物线与双曲线的一个交点为
=1(a>0,b>0)的一个焦点,并与双曲线实轴垂直,已知拋物线与双曲线的一个交点为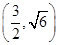 ,求拋物线与双曲线方程.
,求拋物线与双曲线方程.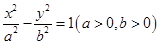 的离心率为2,
的离心率为2,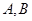 为期左右顶点,点P为双曲线C在第一象限的任意一点,点O为坐标原点,若
为期左右顶点,点P为双曲线C在第一象限的任意一点,点O为坐标原点,若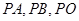 的斜率为
的斜率为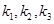 ,则
,则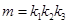 的取值范围为( )
的取值范围为( )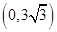
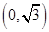
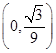
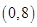
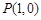 到双曲线
到双曲线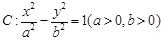 的一条渐近线的距离为
的一条渐近线的距离为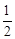 ,则双曲线
,则双曲线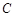 的离心率为 .
的离心率为 .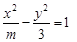 的离心率为2,则
的离心率为2,则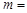 __________.
__________.