题目内容
已知a是给定的实常数.设函数f(x)=(x-a)2(x+b)ex,b∈R,x=a是f(x)的一个极大值点,
(Ⅰ)求b的取值范围;
(Ⅱ)设x1,x2,x3是f(x)的3个极值点,问是否存在实数b,可找到x4∈R,使得x1,x2,x3,x4的某种排列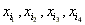 (其中{i1,i2,i3,i4}={1,2,3,4})依次成等差数列?若存在,求所有的b及相应的x4;若不存在,说明理由.
(其中{i1,i2,i3,i4}={1,2,3,4})依次成等差数列?若存在,求所有的b及相应的x4;若不存在,说明理由.
(Ⅰ)求b的取值范围;
(Ⅱ)设x1,x2,x3是f(x)的3个极值点,问是否存在实数b,可找到x4∈R,使得x1,x2,x3,x4的某种排列
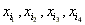 (其中{i1,i2,i3,i4}={1,2,3,4})依次成等差数列?若存在,求所有的b及相应的x4;若不存在,说明理由.
(其中{i1,i2,i3,i4}={1,2,3,4})依次成等差数列?若存在,求所有的b及相应的x4;若不存在,说明理由. 解:(Ⅰ)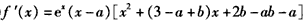 ,
,
令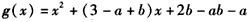 ,
,
则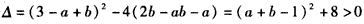 ,
,
于是可设x1,x2是g(x)=0的两实根,且x1<x2,
①当x1=a或x2=a时,则x=a不是f(x)的极值点,此时不合题意;
②当x1≠a且x2≠a时,由于x=a是f(x)的极大值点,故x1<a<x2,即g(a)<0,
即a2+(3-a+b)a+2b-ab-a<0,所以b<-a,
所以b的取值范围是(-∞,-a).
(Ⅱ)由(Ⅰ)可知,假设存在b及x4满足题意,
则①当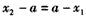 时,则
时,则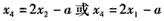 ,
,
于是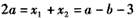 ,
,
即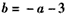 ,
,
此时,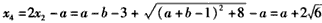 或
或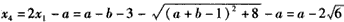 ;
;
②当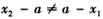 时,则
时,则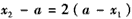 或
或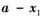
 ,
,
(ⅰ)若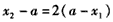 ,则
,则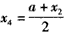 ,
,
于是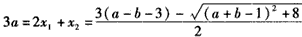 ,
,
即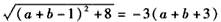 ,
,
于是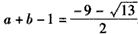 ,
,
此时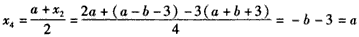
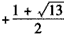 ;
;
(ⅱ)若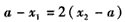 ,则
,则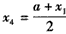 ,
,
于是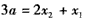
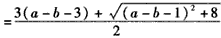 ,
,
即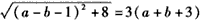 ,
,
于是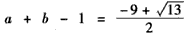 ,
,
此时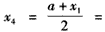
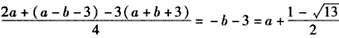 ;
;
综上所述,存在b满足题意;
当b=-a-3时,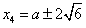 ;
;
当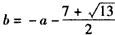 时,
时,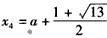 ;
;
当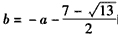 时,
时,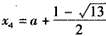 。
。

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目