题目内容
已知数列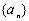 满足
满足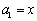 ,
,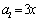 ,
,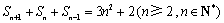 ,
,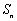 是数列
是数列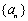 的前
的前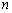 项和.
项和.
(1)若数列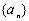 为等差数列.
为等差数列.
(ⅰ)求数列的通项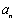 ;
;
(ⅱ)若数列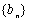 满足
满足 ,数列
,数列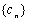 满足
满足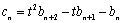 ,试比较数列
,试比较数列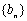 前
前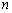 项和
项和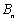 与
与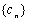 前
前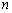 项和
项和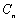 的大小;
的大小;
(2)若对任意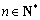 ,
,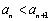 恒成立,求实数
恒成立,求实数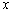 的取值范围.
的取值范围.
(1)(ⅰ)因为 ,所以
,所以 ,
,
即 ,又
,又 ,所以
,所以 , ………………………………2分
, ………………………………2分
又因为数列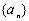 成等差数列,所以
成等差数列,所以 ,即
,即 ,解得
,解得 ,
,
所以 ; ………………………………4分
; ………………………………4分
(ⅱ)因为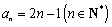 ,所以
,所以 ,其前
,其前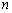 项和
项和 ,
,
又因为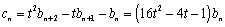 ,………………………………………………5分
,………………………………………………5分
所以其前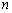 项和
项和 ,所以
,所以 ,…………………7分
,…………………7分
当 或
或 时,
时, ;当
;当 或
或 时,
时, ;
;
当 时,
时, .……………………………………………………………………9分
.……………………………………………………………………9分
(2)由 知
知 ,
,
两式作差,得 ,…………………………………………10分
,…………………………………………10分
所以 ,作差得
,作差得 , ……………11分
, ……………11分
所以,当 时,
时, ;
;
当 时,
时, ;
;
当 时,
时, ;
;
当 时,
时, ;………………14分
;………………14分
因为对任意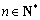 ,
,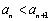 恒成立,所以
恒成立,所以 且
且 ,
,
所以 ,解得,
,解得, ,故实数
,故实数 的取值范围为
的取值范围为 .
.

练习册系列答案
相关题目
 ,则
,则 的最小正周期是 .
的最小正周期是 . 时,求点P距地面的高度PQ;
时,求点P距地面的高度PQ;
 .现从该正三棱锥的六条棱中随机选取两条棱,则这两条棱互相垂直的概率是 .
.现从该正三棱锥的六条棱中随机选取两条棱,则这两条棱互相垂直的概率是 .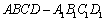 中,
中,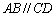 ,
, ,且
,且 .
.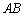 ∥平面
∥平面 ;
;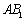 ⊥平面
⊥平面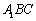 .
.

 (
( 为常数)在
为常数)在 上有最大值3,那么此函数在
上有最大值3,那么此函数在 上任意一点,则点P到直线
上任意一点,则点P到直线 的最小距离为( )
的最小距离为( ) B.
B. C.
C. D.3
D.3 B.
B.  C.
C. D.
D. 