题目内容
(2013•宿迁一模)已知α,β∈(
,
),若sin(α+
)=
,cos(β-
)=
,则sin(α-β)的值为
.
| π |
| 3 |
| 5π |
| 6 |
| π |
| 6 |
| 4 |
| 5 |
| 5π |
| 6 |
| 5 |
| 13 |
| 16 |
| 65 |
| 16 |
| 65 |
分析:由于α-β=(α+
)-(β-
)-π,由α,β∈(
,
),利用两角差的正弦即可求得sin(α-β)的值.
| π |
| 6 |
| 5π |
| 6 |
| π |
| 3 |
| 5π |
| 6 |
解答:解:∵α,β∈(
,
),
∴
<α+
<π,-
<β-
<0,
又sin(α+
)=
,cos(β-
)=
,
∴cos(α+
)=-
,sin(β-
)=-
.
∴sin(α-β)=-sin[(α+
)-(β-
)]
=-[sin(α+
)•cos(β-
)-cos(α+
)•sin(β-
)]
=-[
×
-(-
)×(-
)]
=
.
故答案为:
.
| π |
| 3 |
| 5π |
| 6 |
∴
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| 5π |
| 6 |
又sin(α+
| π |
| 6 |
| 4 |
| 5 |
| 5π |
| 6 |
| 5 |
| 13 |
∴cos(α+
| π |
| 6 |
| 3 |
| 5 |
| 5π |
| 6 |
| 12 |
| 13 |
∴sin(α-β)=-sin[(α+
| π |
| 6 |
| 5π |
| 6 |
=-[sin(α+
| π |
| 6 |
| 5π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
=-[
| 4 |
| 5 |
| 5 |
| 13 |
| 3 |
| 5 |
| 12 |
| 13 |
=
| 16 |
| 65 |
故答案为:
| 16 |
| 65 |
点评:本题考查两角和与差的正弦与余弦,考查观察分析转化运算的能力,属于中档题.

练习册系列答案
相关题目
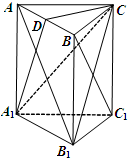 (2013•宿迁一模)如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,BC=BB1,D为AB的中点.
(2013•宿迁一模)如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,BC=BB1,D为AB的中点.