题目内容
设x，y，z∈R且x+2y+3z=1
（I）当z=1，|x+y|+|y+1|＞2时，求x的取值范围；
（II）当x＞0，y＞0，z＞0时，求u=
+
+
的最小值．
（I）当z=1，|x+y|+|y+1|＞2时，求x的取值范围；
（II）当x＞0，y＞0，z＞0时，求u=
| x2 |
| x+1 |
| 2y2 |
| y+2 |
| 3z2 |
| z+3 |
（I）当z=1时，∵x+2y+3z=1，∴x+2y=-2，即y=
∴|x+y|+|y+1|＞2可化简|x-2|+|x|＞4，
∴x＜0时，-x+2-x＞4，∴x＜-1；
0≤x≤2时，-x+2+x＞4不成立；
x＞2时，x-2+x＞4，∴x＞3
综上知，x＜-1或x＞3；
（II）∵（
+
+
）[（x+1）+2（y+2）+3（z+3）]≥（x+2y+3z）2
∴（
+
+
）（x+2y+3z+14）≥（x+2y+3z）2，
∴
+
+
≥
∴u≥
，当且仅当
=
=
，又x+2y+3z=1，即x=
，y=
，z=
时，umin=
．
| -2-x |
| 2 |
∴|x+y|+|y+1|＞2可化简|x-2|+|x|＞4，
∴x＜0时，-x+2-x＞4，∴x＜-1；
0≤x≤2时，-x+2+x＞4不成立；
x＞2时，x-2+x＞4，∴x＞3
综上知，x＜-1或x＞3；
（II）∵（
| x2 |
| x+1 |
| 2y2 |
| y+2 |
| 3z2 |
| z+3 |
∴（
| x2 |
| x+1 |
| 2y2 |
| y+2 |
| 3z2 |
| z+3 |
∴
| x2 |
| x+1 |
| 2y2 |
| y+2 |
| 3z2 |
| z+3 |
| 1 |
| 15 |
∴u≥
| 1 |
| 15 |
| x |
| x+1 |
| y |
| y+2 |
| z |
| z+3 |
| 1 |
| 14 |
| 1 |
| 7 |
| 3 |
| 14 |
| 1 |
| 15 |
练习册系列答案
孟建平小学滚动测试系列答案
黄冈天天练口算题卡系列答案
相关题目
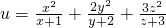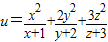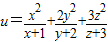的最小值．
的最小值．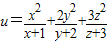
的最小值．
的最小值．