Question

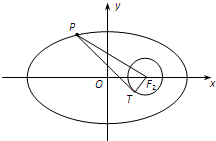已知椭圆

x2

a2

+

y2

b2

=1(a＞b＞c＞0，a2=b2+c2)的左、右焦点分别为F₁，F₂，若以F₂为圆心，b-c为半径作圆F₂，过椭圆上一点P作此圆的切线，切点为T，且|PT|的最小值不小于

3

2

(a-c)．
（1）求椭圆的离心率e的取值范围；
（2）设椭圆的短半轴长为1，圆F₂与x轴的右交点为Q，过点Q作斜率为k（k＞0）的直线l与椭圆相交于A，B两点，若OA⊥OB，求直线l被圆F₂截得的弦长的最大值．

Answer 1

分析：（1）可设且显得的长，当且仅当|PF₂|取得最小值时|PT|取得最小值，进而求得|PF₂|的最小值，进而判断出

(a-c)2-(b-c)2

≥

3

2

(a-c)，求得e的范围．
（2）依题意求得Q点坐标，设出直线方程，与椭圆方程联立消去y，设A（x₁，y₁），B（x₂，y₂），进而表示出x₁+x₂和x₁x₂，代入直线方程求得y₁y₂的表达式和x₁•x₂+y₁•y₂，进而根据OA⊥OB，判断出

OA

•

OB

=0求得k和a的关系，表示出圆心到直线度的距离，根据（1）中e的范围确定c的范围，进而确定S的范围，则其最大值可求．

解答：解：（1）依题意设切线长|PT|=

|PF2|2-(b-c)2

，
∴当且仅当|PF₂|取得最小值时|PT|取得最小值，而|PF₂|_min=a-c，
∴

(a-c)2-(b-c)2

≥

3

2

(a-c)，∴0＜

b-c

a-c

≤

1

2

，从而解得

3

5

≤e＜

2

2

，
故离心率e的取值范围是

3

5

≤e＜

2

2

；
（2）依题意Q点的坐标为（1，0），则直线的方程为y=k（x-1），
联立方程组

y=k(x-1) x2 a2 +y2=1

，得（a²k²+1）x²-2a²k²x+a²k²-a²=0，
设A（x₁，y₁），B（x₂，y₂），则有x1+x2=

2a2k2

a2k2+1

，x1x2=

a2k2-a2

a2k2+1

，
代入直线方程得y₁y₂=k²[x₁x₂-（x₁+x₂）+1]=

k2(1-a2)

a2k2+1

，x1•x2+y1•y2=

k2-a2

a2k2+1

，
又OA⊥OB，∴

OA

•

OB

=0，∴x1x2+y1y2=0，∴k2=a2，∴k=a，直线的方程为ax-y-a=0，
圆心F₂（c，0）到直线l的距离d=

|ac-a|

a2+1

，
由图象可知s=

2d

a

=

2|c-1|

a2+1

=2

c2-2c+1 a2+1

=2

c2-2c+1 c2+2

=2

1- 4 2c+1+ 9 2c+1 -2

，
∴

3

5

≤e＜

2

2

，∴

3

4

≤c＜1，

5

2

≤2c+1＜3，
∴s∈(0，

2 41

41

]，
所以smax=

2 41

41

．

点评：本题主要考查了椭圆的简单性质，直线与圆锥曲线的综合问题，考查了学生数形结合的思想，转化和化归思想的运用．