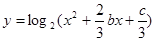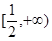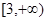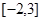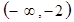题目内容
已知函数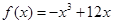 ,①求函数的单调区间;②求函数的极值,③当
,①求函数的单调区间;②求函数的极值,③当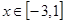 时,求函数的最大值与最小值.
时,求函数的最大值与最小值.
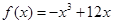 ,①求函数的单调区间;②求函数的极值,③当
,①求函数的单调区间;②求函数的极值,③当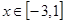 时,求函数的最大值与最小值.
时,求函数的最大值与最小值.见解析.
根据求导公式和求导法则求出函数 的导数,利用函数的单调性与导数的关系,解不等式
的导数,利用函数的单调性与导数的关系,解不等式 得函数的单调增区间,解不等式
得函数的单调增区间,解不等式 <0得函数的单调减区间,然后列表求出其极值与最值.
<0得函数的单调减区间,然后列表求出其极值与最值.
解:① 由
由 ,得
,得 ,
, 函数单调递增;同理,
函数单调递增;同理, 或
或 函数单调递减.
函数单调递减.
②由①得下表:
 极小值=-16,
极小值=-16, 极大值=16.
极大值=16.
③结合①②及 ,得下表:
,得下表:
比较端点函数及极值点的函数值,得 极小值=f(-2)=-16,
极小值=f(-2)=-16,
 的导数,利用函数的单调性与导数的关系,解不等式
的导数,利用函数的单调性与导数的关系,解不等式 得函数的单调增区间,解不等式
得函数的单调增区间,解不等式 <0得函数的单调减区间,然后列表求出其极值与最值.
<0得函数的单调减区间,然后列表求出其极值与最值.解:①
 由
由 ,得
,得 ,
, 函数单调递增;同理,
函数单调递增;同理, 或
或 函数单调递减.
函数单调递减.②由①得下表:
 |  |  |  |  |  |
 | — | 0 | + | 0 | — |
 | 单调递减 | 极小值f(-2) | 单调递增 | 极大值f(2) | 单调递减 |
 极小值=-16,
极小值=-16, 极大值=16.
极大值=16.③结合①②及
 ,得下表:
,得下表: |  |  |  |  |  |
 | | — | 0 | + | |
 | 端点函数值 f(-3)=-9 | 单调 递减 | 极小值f(-2)=-16 | 单调 递增 | 端点函数值 f(1)=11 |
 极小值=f(-2)=-16,
极小值=f(-2)=-16,

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
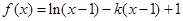
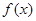 的单调区间;
的单调区间;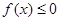 恒成立,试确定实数k的取值范围;
恒成立,试确定实数k的取值范围;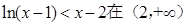 上恒成立
上恒成立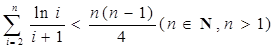
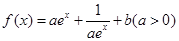
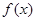 在
在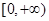 上的最小值;
上的最小值;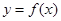 在点
在点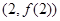 的切线方程为
的切线方程为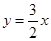 ;求
;求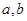 的值。
的值。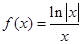
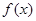 的单调区间; (II)若关于
的单调区间; (II)若关于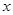 的不等式
的不等式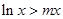 对一切
对一切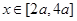 都成立
都成立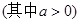 ,求实数
,求实数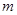 的取值范围.
的取值范围.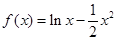 的大致图像是( )
的大致图像是( ) 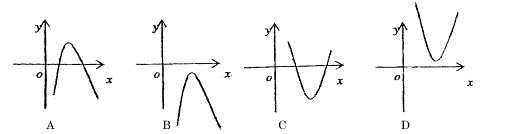
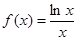 ,若方程
,若方程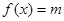 存在两个不同的实数解,则实数
存在两个不同的实数解,则实数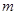 的取值范围为( ▲ )
的取值范围为( ▲ )



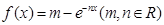
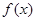 在点x=0处的切线方程为y=x,求m,n的值。
在点x=0处的切线方程为y=x,求m,n的值。 求a的取值范围.
求a的取值范围.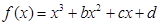 图象如图,则函数
图象如图,则函数