题目内容
【题目】已知函数![]() ,其中
,其中![]() 为常数.
为常数.
(1)当![]() ,且
,且![]() 时,判断函数
时,判断函数![]() 是否存在极值,若存在,求出极值点;若不存在,说明理由;
是否存在极值,若存在,求出极值点;若不存在,说明理由;
(2)若![]() ,对任意的正整数
,对任意的正整数![]() ,当
,当![]() 时,求证:
时,求证:![]() .
.
【答案】(Ⅰ)见解析(Ⅱ)见解析
【解析】试题分析; (1)令![]() ,求出
,求出![]() 的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的极小值即可;
的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的极小值即可;
(Ⅱ)![]() 时,求
时,求![]() 的导数,通过讨论
的导数,通过讨论![]() 是奇数,偶数,结合函数的单调性证明结论即可.
是奇数,偶数,结合函数的单调性证明结论即可.
试题解析:(1)由已知得函数![]() 的定义域为
的定义域为![]() ,
,
当![]() 时,
时,![]() ,所以
,所以![]() ,
,
当![]() 时,由
时,由![]() 得
得![]() ,此时
,此时![]()
当![]() 时,
时,![]() 单调递减;当
单调递减;当![]() 时,
时,![]() 单调递增.
单调递增.
当![]() 时,
时,![]() 在
在![]() 处取得极小值,极小值点为
处取得极小值,极小值点为![]() .
.
(2)证:因为![]() ,所以
,所以![]() .
.
当![]() 为偶数时,令
为偶数时,令![]() ,则
,则![]()
![]() ∴所以
∴所以![]() 当
当![]() 时,
时,![]() 单调递增,
单调递增,![]() 的最小值为
的最小值为![]() .因此
.因此
![]()
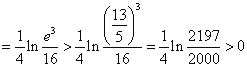
所以![]() 成立.
成立.
当![]() 为奇数时,要证
为奇数时,要证![]() ,由于
,由于![]() ,所以只需证
,所以只需证![]() .
.
令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() 单调递增,又
单调递增,又![]() ,
,
所以当![]() 时,恒有
时,恒有![]() ,命题
,命题![]() 成立.
成立.

练习册系列答案
相关题目
【题目】在中学生综合素质评价某个维度的测评中,分“优秀、合格、尚待改进”三个等级进行学生互评,某校高二年级有男生500人,女生400人,为了了解性别对维度测评结果的影响,采用分层抽样方法从高二年级抽取了45名学生的测评结果,并作出频率统计表如表: 表一:男生测评结果统计
等级 | 优秀 | 合格 | 尚待改进 |
频数 | 15 | x | 5 |
表二:女生测评结果统计
等级 | 优秀 | 合格 | 尚待改进 |
频数 | 15 | 3 | y |
参考数据:
P(K2≥k0) | 0.10 | 0.050 | 0.025 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
(参考公式: ![]() ,其中n=a+b+c+d).
,其中n=a+b+c+d).
(1)计算x,y的值;
(2)由表一表二中统计数据完成2×2列联表,并判断是否有90%的把握认为“测评结果优秀与性别有关”.
男生 | 女生 | 总计 | |
优秀 | |||
非优秀 | |||
总计 |
