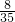Question

在正方体八个顶点中任取四个顺次连接得到三棱锥，则所得三棱锥中至少有三个面都是直角三角形的概率为（ ）
A．
B．
C．
D．

Answer 1

【答案】分析：本题是一个等可能事件的概率，从长方体中任选四个顶点的选法是C₈⁴，能够构成三棱锥的个数有70-12，四个面都是直角三角形的三棱锥有4×6个，三个面是直角的三棱锥有8个，得到概率．
解答：解：由题意知本题是一个等可能事件的概率，
从长方体中任选四个顶点的选法是C₈⁴=70，
∵能够构成三棱锥的个数有70-12=58，
四个面都是直角三角形的三棱锥有4×6=24个，
三个面是直角的三棱锥有8个，
∵能够成三棱锥中至少有三个面都是直角三角形的三棱锥的个数是24+8=32，
∴所求的概率是
故选C．
点评：本题考查等可能事件的概率，考查正方体和三棱锥之间的关系，考查三棱锥的结构特征，本题是以概率为载体，实际上考查立体几何的知识．