题目内容
如图,直线AB与椭圆: (a>b>0)交于A,B两点,与x轴和y轴分别交于点P和点Q,点C是点A关于x轴的对称点,直线BC与x轴交于点R.
(a>b>0)交于A,B两点,与x轴和y轴分别交于点P和点Q,点C是点A关于x轴的对称点,直线BC与x轴交于点R.(1)若点P为(6,0),点Q为(0,3),点A,B恰好是线段QP的两个三等分点.
①求椭圆的方程;
②过坐标原点O引△ABC外接圆的切线,求切线长;
(2)当椭圆给定时,试探究OP•OR是否为定值?若是,请求出此定值;若不是,请说明理由.

【答案】分析:(1)①利用 ,点B为A、P中点,可得点A、B的坐标,代入椭圆方程,求得几何量,从而可求椭圆的方程;
,点B为A、P中点,可得点A、B的坐标,代入椭圆方程,求得几何量,从而可求椭圆的方程;
②确定线段AB的中垂线方程,求得△ABC外接圆的圆心与半径,从而可求切线长;
(2)确定直线BC的方程,求得R的坐标,同理可求P的坐标,表示出OP•OQ,利用P、Q再椭圆上,即可求得结论.
解答:解:(1)①设点A(x,y),由题意知 ,则有(6,-3)=3(x,y-3),
,则有(6,-3)=3(x,y-3),
解得x=2,y=2,即A(2,2),又点B为A、P中点,可得点B(4,1)…(2分)
∴ ,解得:a2=20,b2=5,∴椭圆的方程为
,解得:a2=20,b2=5,∴椭圆的方程为 …(5分)
…(5分)
②由点A(2,2),B(4,1)可求得线段AB的中垂线方程为y=2x- ,令y=0,得x=
,令y=0,得x= .
.
设△ABC外接圆的圆心为M,半径为r,可知M( ,0),r=AM=
,0),r=AM= …(7分)
…(7分)
∴切线长为 …(9分)
…(9分)
(2)设点B(x,y),A(x1,y1),则C(x1,-y1).
所以直线BC的方程为y-y= (x-x),
(x-x),
令y=0,得 ,即点R(
,即点R( ,0),
,0),
同理P( ,0)…(13分)
,0)…(13分)
∴OP•OQ=| ||
|| |=
|= ,
,
又∵ ,∴①×
,∴①× -②×
-②× ,两式相减得
,两式相减得 ,
,
即 ,
,
∴当椭圆给定时,OP•OR为定值a2…(16分)
点评:本题考查椭圆的标准方程,考查直线与圆的位置关系,考查点差法的运用,属于中档题.
 ,点B为A、P中点,可得点A、B的坐标,代入椭圆方程,求得几何量,从而可求椭圆的方程;
,点B为A、P中点,可得点A、B的坐标,代入椭圆方程,求得几何量,从而可求椭圆的方程;②确定线段AB的中垂线方程,求得△ABC外接圆的圆心与半径,从而可求切线长;
(2)确定直线BC的方程,求得R的坐标,同理可求P的坐标,表示出OP•OQ,利用P、Q再椭圆上,即可求得结论.
解答:解:(1)①设点A(x,y),由题意知
 ,则有(6,-3)=3(x,y-3),
,则有(6,-3)=3(x,y-3),解得x=2,y=2,即A(2,2),又点B为A、P中点,可得点B(4,1)…(2分)
∴
 ,解得:a2=20,b2=5,∴椭圆的方程为
,解得:a2=20,b2=5,∴椭圆的方程为 …(5分)
…(5分)②由点A(2,2),B(4,1)可求得线段AB的中垂线方程为y=2x-
 ,令y=0,得x=
,令y=0,得x= .
.设△ABC外接圆的圆心为M,半径为r,可知M(
 ,0),r=AM=
,0),r=AM= …(7分)
…(7分)∴切线长为
 …(9分)
…(9分)(2)设点B(x,y),A(x1,y1),则C(x1,-y1).
所以直线BC的方程为y-y=
 (x-x),
(x-x),令y=0,得
 ,即点R(
,即点R( ,0),
,0),同理P(
 ,0)…(13分)
,0)…(13分)∴OP•OQ=|
 ||
|| |=
|= ,
,又∵
 ,∴①×
,∴①× -②×
-②× ,两式相减得
,两式相减得 ,
,即
 ,
,∴当椭圆给定时,OP•OR为定值a2…(16分)
点评:本题考查椭圆的标准方程,考查直线与圆的位置关系,考查点差法的运用,属于中档题.

练习册系列答案
相关题目
 如图,设点F是椭圆C:
如图,设点F是椭圆C: 如图,直线AB与椭圆:
如图,直线AB与椭圆: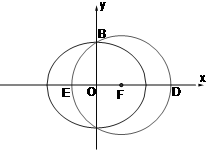 如图,已知F(c,0)是椭圆
如图,已知F(c,0)是椭圆 (a>b>0)交于A,B两点,与x轴和y轴分别交于点P和点Q,点C是点A关于x轴的对称点,直线BC与x轴交于点R.
(a>b>0)交于A,B两点,与x轴和y轴分别交于点P和点Q,点C是点A关于x轴的对称点,直线BC与x轴交于点R.