题目内容
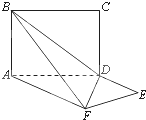 如图,平面ABCD⊥平面ADEF,其中ABCD为矩形,ADEF为梯形,AF∥DE,AF⊥FE,AF=AD=2DE=2,M为AD中点.
如图,平面ABCD⊥平面ADEF,其中ABCD为矩形,ADEF为梯形,AF∥DE,AF⊥FE,AF=AD=2DE=2,M为AD中点.
(Ⅰ) 证明MF⊥BD;
(Ⅱ) 若二面角A-BF-D的平面角的余弦值为 ,求AB的长.
,求AB的长.
(Ⅰ)证明:∵ADEF为梯形,AF∥DE,AF⊥FE,AF=AD=2DE=2,
∴△ADF为正三角形
∵M为AD中点,∴MF⊥AD
∵平面ABCD⊥平面ADEF,平面ABCD∩平面ADEF=AD,
∴MF⊥平面ABCD
∴MF⊥BD;
(Ⅱ)设AB=x.取AF的中点G.

由题意得DG⊥AF.
∵平面ABCD⊥平面ADEF,AB⊥AD,∴AB⊥平面ADEF,∴AB⊥DG.
∴DG⊥平面ABF.
过G作GH⊥BF,垂足为H,连接DH,则DH⊥BF,∴∠DHG为二面角A-BF-D的平面角.
在直角△AGD中,AD=2,AG=1,得DG=
在直角△BAF中,由 =sin∠AFB=
=sin∠AFB= 得
得 ,∴
,∴
在直角△DGH中,DG= ,
, ,∴DH=2
,∴DH=2
∵cos∠DHG= =
= ,∴x=
,∴x=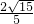 ,∴AB=
,∴AB=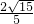
分析:(Ⅰ)证明MF⊥平面ABCD,即可得到结论;
(II)取AF的中点G,过G作GH⊥BF,垂足为H,连接DH,可证得∠DHG为二面角A-BF-D的平面角,解三角形DGH可得答案.
点评:本题考查线面垂直,考查面面角,考查学生的计算能力,正确作出面面角是关键.
∴△ADF为正三角形
∵M为AD中点,∴MF⊥AD
∵平面ABCD⊥平面ADEF,平面ABCD∩平面ADEF=AD,
∴MF⊥平面ABCD
∴MF⊥BD;
(Ⅱ)设AB=x.取AF的中点G.

由题意得DG⊥AF.
∵平面ABCD⊥平面ADEF,AB⊥AD,∴AB⊥平面ADEF,∴AB⊥DG.
∴DG⊥平面ABF.
过G作GH⊥BF,垂足为H,连接DH,则DH⊥BF,∴∠DHG为二面角A-BF-D的平面角.
在直角△AGD中,AD=2,AG=1,得DG=

在直角△BAF中,由
 =sin∠AFB=
=sin∠AFB= 得
得 ,∴
,∴
在直角△DGH中,DG=
 ,
, ,∴DH=2
,∴DH=2
∵cos∠DHG=
 =
= ,∴x=
,∴x=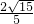 ,∴AB=
,∴AB=
分析:(Ⅰ)证明MF⊥平面ABCD,即可得到结论;
(II)取AF的中点G,过G作GH⊥BF,垂足为H,连接DH,可证得∠DHG为二面角A-BF-D的平面角,解三角形DGH可得答案.
点评:本题考查线面垂直,考查面面角,考查学生的计算能力,正确作出面面角是关键.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
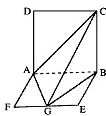 如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且AF=
如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且AF= 如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且
如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且 (2010•河东区一模)如图,平面ABCD⊥平面ABEF,ABCD是正方形.ABEF是矩形,G是线段EF的中点,且B点在平面ACG内的射影在CG上.
(2010•河东区一模)如图,平面ABCD⊥平面ABEF,ABCD是正方形.ABEF是矩形,G是线段EF的中点,且B点在平面ACG内的射影在CG上.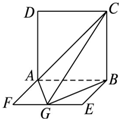 如图,平面ABCD⊥平面ABEF,四边形ABCD是正方形,四边形ABEF是矩形,且AF=
如图,平面ABCD⊥平面ABEF,四边形ABCD是正方形,四边形ABEF是矩形,且AF=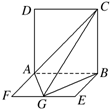 如图,平面ABCD⊥平面ABEF,四边形ABCD是正方形,四边形ABEF是矩形,且AF=
如图,平面ABCD⊥平面ABEF,四边形ABCD是正方形,四边形ABEF是矩形,且AF=