题目内容
已知等差数列{an}的各项均为正数,a1=3,前n项和为Sn,{bn}是等比数列,b1=1,且b2S2=64,b3S3=960.
(1)求数列{an}与{bn}的通项公式;
(2)求证: 都成立.
都成立.
解:(1)设{an}的公差为d(d>0),{bn}的公比为q,
则
解得 (舍)
(舍)
所以an=3+2(n-1)=2n+1,n∈N*,
bn=8n-1,n∈N*.
(2)因为Sn=3+5+…+(2n+1)=n(n+2)
所以 =
=
=
= .
.
故 都成立.
都成立.
分析:(1)因为数列{an}为等差数列,所以只要求出首项与公差,就可以求出通项公式,同样,因为数列{an}为等比数列,所以只要求出首项与公比,就可以求出通项公式,然后根据a1=3,前n项和为Sn,{bn}是等比数列,b1=1,且b2S2=64,b3S3=960.寻找含a1,d,b1,q的关系式,求出a1,d,b1,q即可.
(2)由(1)中所求数列{an}的首项与公差,代入等差数列的前n项和公式,求出Sn,再计算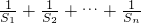 ,最后用放缩法即可证明.
,最后用放缩法即可证明.
点评:本题考查了等差等比数列通项公式的求法,以及放缩法比较大小.
则

解得
 (舍)
(舍) 所以an=3+2(n-1)=2n+1,n∈N*,
bn=8n-1,n∈N*.
(2)因为Sn=3+5+…+(2n+1)=n(n+2)
所以
 =
=
=

=
 .
.故
 都成立.
都成立.分析:(1)因为数列{an}为等差数列,所以只要求出首项与公差,就可以求出通项公式,同样,因为数列{an}为等比数列,所以只要求出首项与公比,就可以求出通项公式,然后根据a1=3,前n项和为Sn,{bn}是等比数列,b1=1,且b2S2=64,b3S3=960.寻找含a1,d,b1,q的关系式,求出a1,d,b1,q即可.
(2)由(1)中所求数列{an}的首项与公差,代入等差数列的前n项和公式,求出Sn,再计算
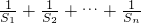 ,最后用放缩法即可证明.
,最后用放缩法即可证明.点评:本题考查了等差等比数列通项公式的求法,以及放缩法比较大小.

练习册系列答案
相关题目
 已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.
已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.