题目内容
3.从4位老师中选出3人到3个班级上课,每人任教1个班级,共有24种不同的选法.分析 选3名教师分配到三个班级中即可,问题得以解决.
解答 解:从4位老师中选出3人到3个班级上课,每人任教1个班级,选3名教师分配到三个班级中,故有A43=24种,
故答案为:24.
点评 本题考查了简单的排列组合问题,属于基础题.

练习册系列答案
相关题目
13.下面是关于复数z=$\frac{2}{1+i}$的四个命题:
p1:复数z的共轭复数为1+i;
p2:复数z的虚部为1;
p3:复数z对应的点在第四象限;
p4:|z|=$\sqrt{2}$.
其中真命题的个数为( )
p1:复数z的共轭复数为1+i;
p2:复数z的虚部为1;
p3:复数z对应的点在第四象限;
p4:|z|=$\sqrt{2}$.
其中真命题的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
13.某同学用“五点法”画函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<$\frac{π}{2}$)在某一个周期的图象时,列表并填入的部分数据如下表:
(Ⅰ)求x1,x2,x3的值及函数f(x)的表达式;
(Ⅱ)将函数f(x)的图象向左平移π个单位,可得到函数g(x)的图象,若直线y=k与函数y=f(x)g(x)的图象在[0,π]上有交点,求实数k的取值范围.
| x | $\frac{2π}{3}$ | x1 | $\frac{8π}{3}$ | x2 | x3 |
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| Asin(ωx+φ) | 0 | 2 | 0 | -2 | 0 |
(Ⅱ)将函数f(x)的图象向左平移π个单位,可得到函数g(x)的图象,若直线y=k与函数y=f(x)g(x)的图象在[0,π]上有交点,求实数k的取值范围.
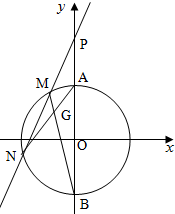 已知A,B为圆O:x2+y2=4与y轴的交点(A在B上),过点P(0,4)的直线l交圆O于M,N两点.
已知A,B为圆O:x2+y2=4与y轴的交点(A在B上),过点P(0,4)的直线l交圆O于M,N两点. 如图,有一景区的平面图是一个半圆形,其中O为圆心,直径AB的长为2km,C,D两点在半圆弧上,且BC=CD,设∠COB=θ;
如图,有一景区的平面图是一个半圆形,其中O为圆心,直径AB的长为2km,C,D两点在半圆弧上,且BC=CD,设∠COB=θ;