Question

椭圆=1(a＞b＞0)的左、右焦点为F₁、F₂，过F₁的直线l与椭圆交于A、B两点.

(1)如果点A在圆x²+y²=c²(c为椭圆的半焦距)上，且|F₁A|=c，求椭圆的离心率；

(2)若函数y=+log_mx(m＞0且m≠1)的图象，无论m为何值时恒过定点(b，a)，求·的取值范围.

Answer 1

解:(1)∵点A在圆x²+y²=c²上,∴△AF₁F₂为一直角三角形.

∵|F₁A|=c,|F₁F₂|=2c,

∴|F₂A|==c.

由椭圆的定义,知|AF₁|+|AF₂|=2a，∴c+3c=2a.∴e==3-1.

(2)∵函数y=+log_mx的图象恒过点(1,),∴a=,b=1,c=1,

点F₁(－1，0)，F₂(1，0).

①若AB⊥x轴,则A(-1,),B(-1,)，

∴=(-2,),=(-2,),·=4=.

②若AB与x轴不垂直，设直线AB的斜率为k，则AB的方程为y=k(x+1).

由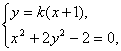消去y得(1+2k²)x²+4k²x+2(k²-1)=0.(*)

∵Δ=8k²+8＞0,∴方程(*)有两个不同的实根.

设点A(x₁，y₁)，B(x₂，y₂)，则x₁，x₂是方程(*)的两个根.

x₁+x₂=,x₁x₂=.

=(x₁-1,y₁),=(x₂-1,y₂),·=(x₁-1)(x₂-1)+y₁y₂=(1+k²)x₁x₂+(k²-1)(x₁+x₂)+1+k²

=(1+k²)+(k²-1)()+1+k²=.

∵1+2k²≥1,∴0＜≤1,0＜≤,-1≤·=＜.

由①②知-1≤·＜.