题目内容
(本小题10分)
已知圆C过点M(0,-2)、N(3,1),且圆心C在直线x+2y+1=0上.
(1)求圆C的方程;
(2)设直线ax-y+1=0与圆C交于A,B两点,是否存在实数a,使得过点P(2,0)的直线l垂直平分弦AB?若存在,求出实数a的值;若不存在,请说明理由.
(本小题10分)
解:(1)设圆C的方程为:x2+y2+Dx+Ey+F=0
则有 …………………2分
…………………2分
解得 ……………………………4分
……………………………4分
∴圆C的方程为:x2+y2-6x+4y+4=0 …………5分
(2)设符合条件的实数![]() 存在,
存在,
由于l垂直平分弦![]() ,故圆心
,故圆心![]() 必在l上.
必在l上.
所以l的斜率![]() ,
,
而![]() , 所以
, 所以![]() . …………7分
. …………7分
把直线ax-y+1=0 即y=ax +1.代入圆![]() 的方程,
的方程,
消去![]() ,整理得
,整理得![]() .
.
由于直线![]() 交圆
交圆![]() 于
于![]() 两点,
两点,
故![]() ,
,
即![]() ,解得
,解得![]() .
.
则实数![]() 的取值范围是
的取值范围是![]() .…………………9分
.…………………9分
由于![]() ,
,
故不存在实数![]() ,使得过点
,使得过点![]() 的直线l垂直平分弦
的直线l垂直平分弦![]() .………10分
.………10分

练习册系列答案
相关题目
 当
当 时,求不等式
时,求不等式 的解集;若
的解集;若 的解集包含
的解集包含 ,求a的取值范围。
,求a的取值范围。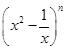 展开式中的二项式系数的和比
展开式中的二项式系数的和比 展开式的二项式系数的和大
展开式的二项式系数的和大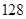 ,求
,求

 且
且 ,求以N(1,1)为圆心,并且与
,求以N(1,1)为圆心,并且与 相切的圆的方程.
相切的圆的方程. 点
点 是
是 的重心,过点
的重心,过点 与
与 分别交于
分别交于 两点.
两点. 表示
表示 ;
; 试问
试问 是否为定值,证明你的结论.
是否为定值,证明你的结论.