题目内容
设数列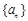 为等比数列,数列
为等比数列,数列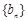 满足
满足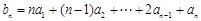 ,
, ,已知
,已知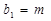 ,
, ,其中
,其中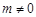 .
.
(Ⅰ)求数列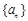 的首项和公比;
的首项和公比;
(Ⅱ)当m=1时,求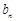 ;
;
(Ⅲ)设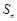 为数列
为数列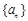 的前
的前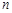 项和,若对于任意的正整数
项和,若对于任意的正整数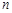 ,都有
,都有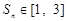 ,求实数
,求实数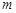 的取值范围.
的取值范围.
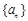 为等比数列,数列
为等比数列,数列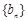 满足
满足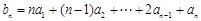 ,
, ,已知
,已知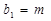 ,
, ,其中
,其中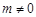 .
.(Ⅰ)求数列
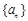 的首项和公比;
的首项和公比;(Ⅱ)当m=1时,求
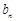 ;
;(Ⅲ)设
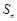 为数列
为数列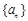 的前
的前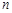 项和,若对于任意的正整数
项和,若对于任意的正整数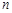 ,都有
,都有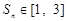 ,求实数
,求实数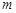 的取值范围.
的取值范围.见解析
(1)根据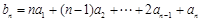 及
及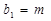 ,
, 将减少变量,
将减少变量,
求得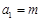 ,
,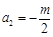 故
故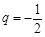 ;
;
(2)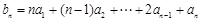 当m=1时既是等比数列
当m=1时既是等比数列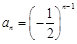 与等差数列
与等差数列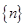 组成的差比数列的前n项和,
组成的差比数列的前n项和,
错位相减法得之: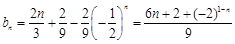
(Ⅲ)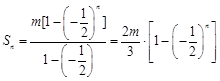 是数列
是数列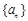 为等比数列的和;
为等比数列的和;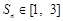
 分类讨论
分类讨论
解(Ⅰ)由已知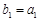 ,所以
,所以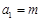 ;…………1分
;…………1分
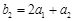 ,所以
,所以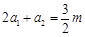 ,解得
,解得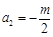 ;
;
所以数列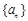 的公比
的公比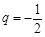 ;…………3分(Ⅱ)当
;…………3分(Ⅱ)当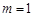 时,
时,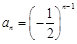 ,…………1分
,…………1分
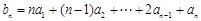 ,………………………①,
,………………………①,
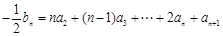 ,……………………②,
,……………………②,
②-①得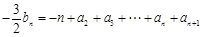 ,………3分
,………3分
所以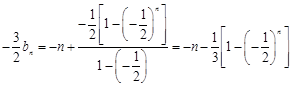 ,
,
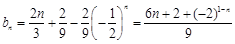 .…………5分
.…………5分
(Ⅲ)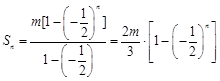 ,…………1分
,…………1分
因为 ,所以由
,所以由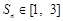 得
得 ,………2分
,………2分
注意到,当n为奇数时,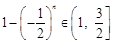 ;当
;当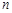 为偶数时,
为偶数时,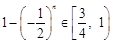 ,
,
所以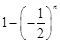 最大值为
最大值为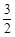 ,最小值为
,最小值为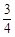 .…………4分
.…………4分
对于任意的正整数n都有 ,
,
所以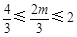 ,解得
,解得
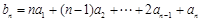 及
及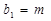 ,
, 将减少变量,
将减少变量,求得
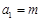 ,
,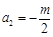 故
故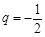 ;
;(2)
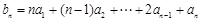 当m=1时既是等比数列
当m=1时既是等比数列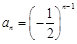 与等差数列
与等差数列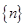 组成的差比数列的前n项和,
组成的差比数列的前n项和,错位相减法得之:
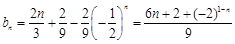
(Ⅲ)
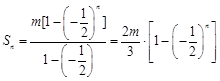 是数列
是数列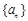 为等比数列的和;
为等比数列的和;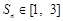
 分类讨论
分类讨论解(Ⅰ)由已知
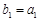 ,所以
,所以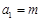 ;…………1分
;…………1分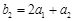 ,所以
,所以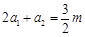 ,解得
,解得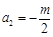 ;
;所以数列
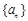 的公比
的公比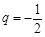 ;…………3分(Ⅱ)当
;…………3分(Ⅱ)当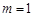 时,
时,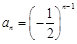 ,…………1分
,…………1分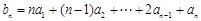 ,………………………①,
,………………………①,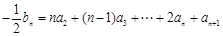 ,……………………②,
,……………………②,②-①得
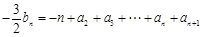 ,………3分
,………3分所以
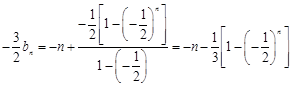 ,
,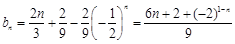 .…………5分
.…………5分(Ⅲ)
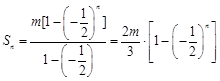 ,…………1分
,…………1分因为
 ,所以由
,所以由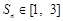 得
得 ,………2分
,………2分注意到,当n为奇数时,
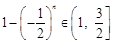 ;当
;当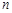 为偶数时,
为偶数时,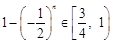 ,
,所以
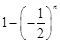 最大值为
最大值为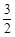 ,最小值为
,最小值为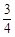 .…………4分
.…………4分对于任意的正整数n都有
 ,
,所以
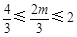 ,解得
,解得

练习册系列答案
相关题目
 的前n项和为
的前n项和为 ,
, ,
, ,则此等比数列的公比q=
,则此等比数列的公比q=  ,将数列
,将数列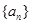 的各项依次从上到下、从左到右排成如图三角形数表,其中第i行有
的各项依次从上到下、从左到右排成如图三角形数表,其中第i行有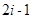
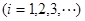 个数,则第10行第8个数是 .
个数,则第10行第8个数是 . 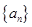 的前
的前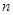 项和为
项和为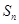 ,
, 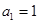 ,且
,且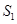 ,
,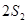 ,
,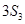 成等差数列.
成等差数列.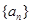 通项公式;
通项公式;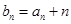 ,求数列
,求数列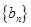 前
前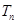 .
. ,
,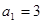 ,
, ,则
,则 与
与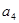 的等比中项等于----.
的等比中项等于----.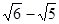 与
与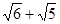 的等比中项是 ( )
的等比中项是 ( ) 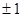
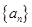 的前
的前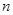 项和
项和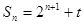 , 则常数
, 则常数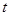 的取值是( )
的取值是( ) 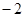
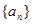 各项为正,若
各项为正,若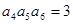 ,则
,则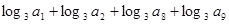 的值为:( )
的值为:( )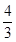



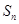 为等比数列
为等比数列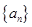 的前
的前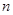 项和,已知
项和,已知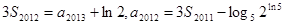 ,则公比
,则公比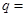 ( )
( )