题目内容
若双曲线 的一个焦点到一条渐近线的距离等于焦距的
的一个焦点到一条渐近线的距离等于焦距的 ,则该双曲线的离心率为( )
,则该双曲线的离心率为( )A.

B.

C.

D.

【答案】分析:因为双曲线即关于两条坐标轴对称,又关于原点对称,所以任意一个焦点到两条渐近线的距离都相等,所以不妨利用点到直线的距离公式求(c,0)到y=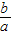 x的距离,再令该距离等于焦距的
x的距离,再令该距离等于焦距的 ,就可得到含b,c的齐次式,再把b用a,c表示,利用e=
,就可得到含b,c的齐次式,再把b用a,c表示,利用e=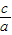 即可求出离心率.
即可求出离心率.
解答:解:双曲线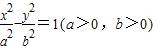 的焦点坐标为(c,0)(-c,0),渐近线方程为y=±
的焦点坐标为(c,0)(-c,0),渐近线方程为y=±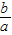 x
x
根据双曲线的对称性,任意一个焦点到两条渐近线的距离都相等,
求(c,0)到y=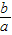 x的距离,d=
x的距离,d=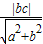 =
=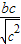 =b,
=b,
又∵焦点到一条渐近线的距离等于焦距的 ,
,
∴b= ×2c,两边平方,得4b2=c2,即4(c2-a2)=c2,
×2c,两边平方,得4b2=c2,即4(c2-a2)=c2,
∴3c2=4a2,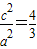 ,即e2=
,即e2= ,e=
,e=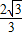
故选B
点评:本题主要考查点到直线的距离公式的应用,以及双曲线离心率的求法,求离心率关键是找到a,c的齐次式.
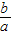 x的距离,再令该距离等于焦距的
x的距离,再令该距离等于焦距的 ,就可得到含b,c的齐次式,再把b用a,c表示,利用e=
,就可得到含b,c的齐次式,再把b用a,c表示,利用e=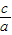 即可求出离心率.
即可求出离心率.解答:解:双曲线
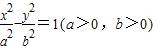 的焦点坐标为(c,0)(-c,0),渐近线方程为y=±
的焦点坐标为(c,0)(-c,0),渐近线方程为y=±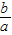 x
x根据双曲线的对称性,任意一个焦点到两条渐近线的距离都相等,
求(c,0)到y=
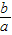 x的距离,d=
x的距离,d=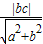 =
=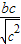 =b,
=b,又∵焦点到一条渐近线的距离等于焦距的
 ,
,∴b=
 ×2c,两边平方,得4b2=c2,即4(c2-a2)=c2,
×2c,两边平方,得4b2=c2,即4(c2-a2)=c2,∴3c2=4a2,
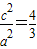 ,即e2=
,即e2= ,e=
,e=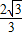
故选B
点评:本题主要考查点到直线的距离公式的应用,以及双曲线离心率的求法,求离心率关键是找到a,c的齐次式.

练习册系列答案
相关题目
 的一个焦点到一条渐近线的距离等于焦距的
的一个焦点到一条渐近线的距离等于焦距的 ,则该双曲线的渐近线方程是( )
,则该双曲线的渐近线方程是( ) B.
B. C.
C. D.
D.
 的一个焦点到一条渐近线的距离等于焦距的
的一个焦点到一条渐近线的距离等于焦距的 ,则该双曲线的离心率是
,则该双曲线的离心率是 B.
B. C.
C. D.
D.
 的一个焦点到一条渐近线的距离等于焦距的
的一个焦点到一条渐近线的距离等于焦距的 ,则该双曲线的渐近线方程是 ( )
,则该双曲线的渐近线方程是 ( ) B.
B. C.
C. D.
D.
 的一个焦点到一条渐近线的距离等于焦距的
的一个焦点到一条渐近线的距离等于焦距的 ,则该双曲线的渐近线方程是 ( )
,则该双曲线的渐近线方程是 ( ) B.
B. C.
C. D.
D.