题目内容
已知{an}为等比数列，且a3+a6=36，a4+a7=18．
（1）若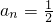
，求n；
（2）设数列{an}的前n项和为Sn，求S8．
解：（1）设等比数列{an}的公比为q则an=a1qn-1
∵a3+a6=36，a4+a7=18
∴
∴
∴
∵
∴
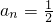
∴n=9
（2）由（1）可得
∴
分析：（1）设等比数列{an}的公比为q根据条件a3+a6=36，a4+a7=18利用等比数列的通项公式可求出首项和公比再利用条件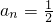即可求出n．
（2）在第一问的基础上直接利用等比数列的前n项和公式即可求出S8．
点评：本题主要考察了等比数列的通项公式和前n项和公式的应用．解题的关键是熟记等比数列的通项公式an=a1qn-1
和前n项和公式
（q≠1）!
∵a3+a6=36，a4+a7=18
∴
∴
∴
∵
∴
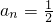
∴n=9
（2）由（1）可得
∴
分析：（1）设等比数列{an}的公比为q根据条件a3+a6=36，a4+a7=18利用等比数列的通项公式可求出首项和公比再利用条件
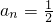即可求出n．（2）在第一问的基础上直接利用等比数列的前n项和公式即可求出S8．
点评：本题主要考察了等比数列的通项公式和前n项和公式的应用．解题的关键是熟记等比数列的通项公式an=a1qn-1
和前n项和公式
（q≠1）! 
练习册系列答案
相关题目