Question

已知f（x）=lnx-x²+bx+3．
（Ⅰ）若函数f（x）在点（2，y）处的切线与直线2x+y+2=0垂直，求函数f（x）在区间[1，3]上的最小值；
（Ⅱ）若f（x）在区间[1，m]上单调，求b的取值范围．

Answer 1

分析：（Ⅰ）首先求出函数的导数f′（x），令x=2求出函数f（x）在点（2，y）的斜率，然后根据函数f（x）在点（2，y）处的切线与直线2x+y+2=0垂直，求出函数f（x）的表达式，根据导数判断函数的单调性，从而求函数f（x）在区间[1，3]上的最小值；
（Ⅱ）由（Ⅰ）求出函数的单调区间，可知y=2x-

1

x

在[1，m]上单调递增，在[1，m]上恒成立，从而求出b的取值范围．

解答：解：（1）f′(x)=

1

x

-2x+b直线2x+y+2=0斜率为-2，
令f′（2）=

1

2

得b=4，∴f（x）=lnx-x²+4x+3
∴f′(x)=

1

x

-2x+4=

-2x2+4x+1

x

=0得x=

2± 6

2

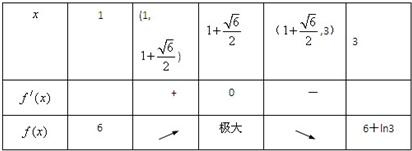
∵6+ln3＞6，∴x=1时，f（x）在[1，3]上最小值6；（6分）
（2）令f′(x)=

1

x

-2x+b≥0得b≥2x-

1

x

，
在[1，m]上恒成立而y=2x-

1

x

在[1，m]上单调递增，
最大值为2m-

1

m

，∴b≥2m-

1

m

令f′(x)=

1

x

-2x+b≤0得b≤2x-

1

x

，
在[1，m]上恒成立而y=2x-

1

x

在[1，m]单调递增，最小值为y=1，
∴b≤1
故b≥2m-

1

m

或b≤1时f（x）在[1，m]上单调． （12分）

点评：此题主要考查函数导数与函数单调性之间的关系，需要掌握并会熟练运用导数判断函数的单调性．