题目内容
已知单调递增的等比数列 满足:
满足: ,且
,且 是
是 、
、 的等差中项.
的等差中项.
(1)求数列 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列 的前
的前 项和
项和 .
.
【答案】
(1)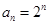 ;(2)
;(2)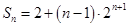 .
.
【解析】
试题分析:(1)先由条件“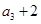 是
是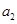 ,
,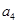 的等差中项”得到
的等差中项”得到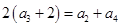 ,即
,即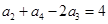 ,然后利用首项
,然后利用首项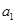 和公比
和公比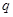 将相关的等式表示,构建二元方程组,求出首项
将相关的等式表示,构建二元方程组,求出首项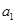 和公比
和公比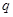 的值,从而确定数列
的值,从而确定数列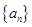 的通项公式;(2)先求出数列
的通项公式;(2)先求出数列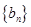 的通项公式,根据数列
的通项公式,根据数列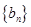 的通项公式选择错位相减法求数列
的通项公式选择错位相减法求数列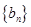 的前
的前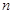 项和
项和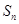 .
.
试题解析:(1)由题意知: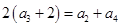 ,即
,即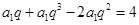 ,
,
又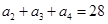 ,即
,即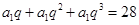 ,
,
所以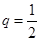 (不合题意)或
(不合题意)或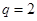 ,
,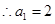 ,
故
,
故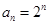 ;
;
(2)由(1)知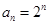 ,
,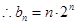 ,
,
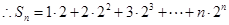 ,
,
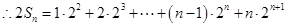
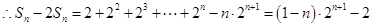 ,
,
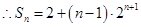 .
.
考点:1.等比数列的通项公式;2.错位相减法

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目