题目内容
(12分)已知定义域为R的函数 是奇函数.
是奇函数.
(1)求 的值;
的值;
(2)若对任意的 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围.
(1)a=2,b=1;(2)k≥5
【解析】
试题分析:(1)因为f(x)是R上的奇函数,所以f(0)=0,即 ,解得b=1
,解得b=1
从而有 又由
又由 ,知
,知 ,解得a=2 -----5分
,解得a=2 -----5分
(2)由(1)知
易知f(x)在R上为减函数因f(x)是奇函数,从而不等式
 等价于
等价于
因f(x)是R上的减函数, 由上式推得 
即对一切 恒成立,从而
恒成立,从而 -----7分
-----7分
考点:本题考查函数的奇偶性,函数的单调性

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目

 B.
B. C.
C.  D.
D.
 ,则
,则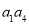 =( )
=( ) 在区间
在区间 上的零点个数为( )
上的零点个数为( )  ,则
,则 等于( )
等于( ) B.
B. C.
C. D.R
D.R 与
与 的夹角为
的夹角为 ,若(
,若( )
) (
( ),则
),则 .
. ,且
,且 ,则
,则 的值是( ).
的值是( ). B.
B.
 D.随
D.随 取不同值而取不同值
取不同值而取不同值

 是( )
是( ) 的偶函数 (B)最小正周期为
的偶函数 (B)最小正周期为 的偶函数 (D)最小正周期为
的偶函数 (D)最小正周期为