Question

已知直线l：mx-2y+2m=0（m∈R）和椭圆C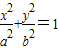：（a＞b＞0），椭圆C的离心率为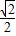，连接椭圆的四个顶点形成四边形的面积为2．
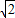（I）求椭圆C的方程；
（II）设直线l经过的定点为Q，过点Q作斜率为k的直线l′与椭圆C有两个不同的交点，求实数k的取值范围；
（Ⅲ）设直线l与y轴的交点为P，M为椭圆C上的动点，线段PM长度的最大值为f（m），求f（m）的表达式．

Answer 1

【答案】分析：（I）直接利用离心率为，以及连接椭圆的四个顶点形成四边形的面积为2列出关于a，b，c方程，求出a，b，c即可得到椭圆方程；
（II）先求出直线所过的顶点坐标，再联立直线方程与椭圆方程，利用判别式大于0即可求实数k的取值范围；
（Ⅲ）先求出点P的坐标（0，m），设出点M，根据两点间的距离公式求出|PM|²的表达式，根据M为椭圆C上的动点的限制对m分情况讨论即可求出f（m）的表达式．
解答：解：（I）由离心率，得
又因为，所以，即椭圆标准方程为．（4分）
（II）由l：mx-2y+2m=0经过定点Q（-2，0），则直线l′：y=k（x+2），
由 有（2k²+1）x²+8k²x+8k²-2=0．
所以△=64k⁴-8（2k²+1）（4k²-1）＞0，可化为 2k²-1＜0
解得． （8分）
（Ⅲ） 由l：mx-2y+2m=0，设x=0，则y=m，所以P（0，m）．
设M（x，y）满足，
则|PM|²=x²+（y-m）²=2-2y²+（y-m ）²=-y²-2my+m²+2=-（y+m）²+2m²+2，
因为-1≤y≤1，所以
当|m|＞1时，|MP|的最大值f（m）=1+|m|；
当|m|≤1时，|MP|的最大值f（m）=；
所以f（m）=．（12分）
点评：本小题主要考查椭圆的标准方程和几何性质、直线的方程、两点间的距离公式等基础知识，考查用代数方法研究圆锥曲线的性质及数形结合的思想，考查综合分析与运算能力．