题目内容
椭圆的长轴长为20，短轴长为16，则椭圆上的点到椭圆中心距离的范围是（ ）
分析：根据椭圆的几何性质，结合题中的数据加以计算，即可得到本题答案．
解答：解：设椭圆的方程为
+
=1(a＞b＞0)
∵椭圆的长轴长为20，短轴长为16，
∴2a=20且2b=16，得a=10且b=8
根据椭圆的几何性质，得
该椭圆上的点到椭圆中心距离d∈[b，a]，即d∈[8，10]
故选：B
| x2 |
| a2 |
| y2 |
| b2 |
∵椭圆的长轴长为20，短轴长为16，
∴2a=20且2b=16，得a=10且b=8
根据椭圆的几何性质，得
该椭圆上的点到椭圆中心距离d∈[b，a]，即d∈[8，10]
故选：B
点评：本题给出椭圆的长轴、短轴的大小．求椭圆上的点到椭圆中心距离的范围．着重考查了椭圆的标准方程与简单几何性质等知识，属于基础题．
练习册系列答案
相关题目
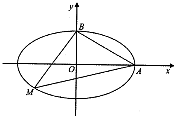（2012•厦门模拟）某公园内有一椭圆形景观水池，经测量知，椭圆长轴长为20米，短轴长为16米．现以椭圆长轴所在直线为x轴，短轴所在直线为y轴，建立平面直角坐标系，如图所示．
轴，短轴所在直线为
轴，建立平面直角坐标系，如图所示：