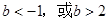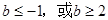题目内容
已知函数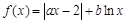 (
(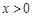 ).
).
(1)若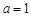 ,
,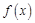 在
在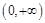 上是单调增函数,求
上是单调增函数,求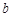 的取值范围;
的取值范围;
(2)若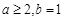 ,求方程
,求方程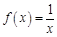 在
在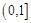 上解的个数.
上解的个数.
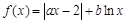 (
(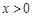 ).
).(1)若
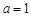 ,
,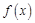 在
在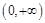 上是单调增函数,求
上是单调增函数,求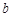 的取值范围;
的取值范围;(2)若
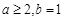 ,求方程
,求方程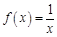 在
在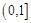 上解的个数.
上解的个数.(1)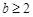 .
.
(2)当a≥3时,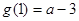 ≥0,∴g(x)=0在
≥0,∴g(x)=0在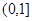 上有惟一解.
上有惟一解.
当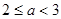 时,
时,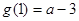 <0,∴g(x)=0在
<0,∴g(x)=0在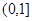 上无解.
上无解.
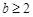 .
. (2)当a≥3时,
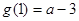 ≥0,∴g(x)=0在
≥0,∴g(x)=0在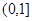 上有惟一解.
上有惟一解.当
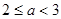 时,
时,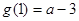 <0,∴g(x)=0在
<0,∴g(x)=0在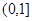 上无解.
上无解. (1)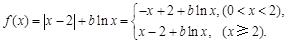 然后分别研究
然后分别研究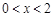 时,
时,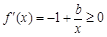 恒成立且
恒成立且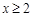 时,
时,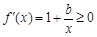 恒成立时b的取值范围即可.
恒成立时b的取值范围即可.
(2) 构造函数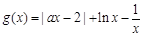 ,即
,即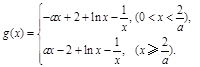
分别研究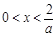 和
和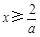 上的单调性,极值和最值.做出草图,数形结合解决即可
上的单调性,极值和最值.做出草图,数形结合解决即可
(1)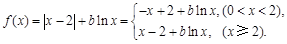 …………………2分
…………………2分
①当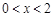 时,
时, 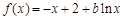 ,
,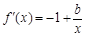 .
.
由条件,得 恒成立,即
恒成立,即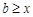 恒成立,∴
恒成立,∴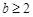 . ……………………4分
. ……………………4分
②当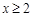 时,
时,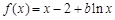 ,
,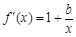 .
.
由条件,得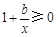 恒成立,即
恒成立,即 恒成立,∴b≥-2.
恒成立,∴b≥-2.
综合①,②得b的取值范围是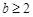 . ……………6分
. ……………6分
(2)令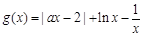 ,即
,即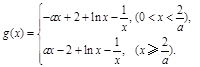 ………………8分
………………8分
当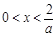 时,
时,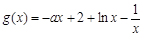 ,
,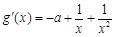 .
.
∵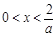 ,∴
,∴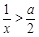 .则
.则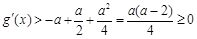 .
.
即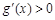 ,∴
,∴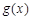 在(0,
在(0,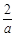 )上是递增函数.………………………10分
)上是递增函数.………………………10分
当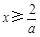 时,
时,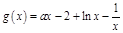 ,
,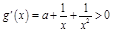 .
.
∴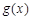 在(
在(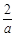 ,+∞)上是递增函数.
,+∞)上是递增函数.
又因为函数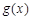 在
在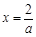 有意义,∴
有意义,∴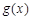 在(0,+∞)上是递增函数.………12分
在(0,+∞)上是递增函数.………12分
∵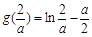 ,而
,而 ,∴
,∴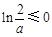 ,则
,则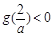 .∵a≥2,
.∵a≥2,
∴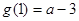 , ……14分
, ……14分
当a≥3时,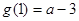 ≥0,∴g(x)=0在
≥0,∴g(x)=0在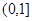 上有惟一解.
上有惟一解.
当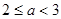 时,
时,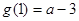 <0,∴g(x)=0在
<0,∴g(x)=0在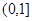 上无解
上无解
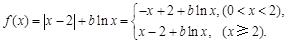 然后分别研究
然后分别研究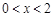 时,
时,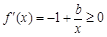 恒成立且
恒成立且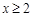 时,
时,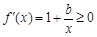 恒成立时b的取值范围即可.
恒成立时b的取值范围即可.(2) 构造函数
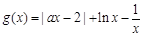 ,即
,即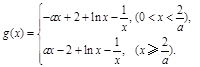
分别研究
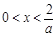 和
和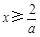 上的单调性,极值和最值.做出草图,数形结合解决即可
上的单调性,极值和最值.做出草图,数形结合解决即可(1)
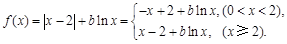 …………………2分
…………………2分①当
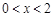 时,
时, 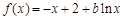 ,
,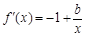 .
.由条件,得
 恒成立,即
恒成立,即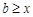 恒成立,∴
恒成立,∴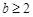 . ……………………4分
. ……………………4分②当
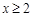 时,
时,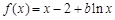 ,
,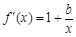 .
.由条件,得
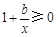 恒成立,即
恒成立,即 恒成立,∴b≥-2.
恒成立,∴b≥-2. 综合①,②得b的取值范围是
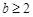 . ……………6分
. ……………6分(2)令
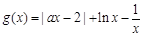 ,即
,即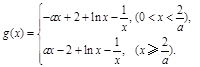 ………………8分
………………8分当
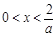 时,
时,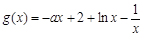 ,
,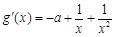 .
.∵
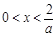 ,∴
,∴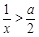 .则
.则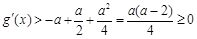 .
.即
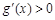 ,∴
,∴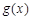 在(0,
在(0,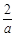 )上是递增函数.………………………10分
)上是递增函数.………………………10分当
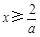 时,
时,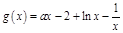 ,
,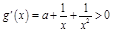 .
.∴
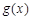 在(
在(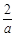 ,+∞)上是递增函数.
,+∞)上是递增函数.又因为函数
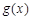 在
在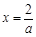 有意义,∴
有意义,∴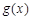 在(0,+∞)上是递增函数.………12分
在(0,+∞)上是递增函数.………12分∵
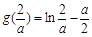 ,而
,而 ,∴
,∴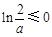 ,则
,则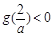 .∵a≥2,
.∵a≥2,∴
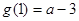 , ……14分
, ……14分当a≥3时,
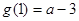 ≥0,∴g(x)=0在
≥0,∴g(x)=0在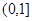 上有惟一解.
上有惟一解.当
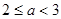 时,
时,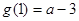 <0,∴g(x)=0在
<0,∴g(x)=0在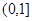 上无解
上无解
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
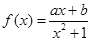 是定义在
是定义在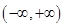 上的奇函数,且
上的奇函数,且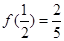 。
。 的解析式;
的解析式; ,其中
,其中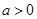
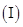 若
若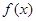 在x=1处取得极值,求a的值;
在x=1处取得极值,求a的值; 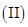 求
求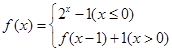 ,则
,则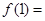 ( )
( )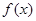 在
在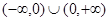 上有意义,且在
上有意义,且在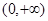 上是增函数,
上是增函数,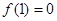
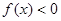 的实数
的实数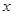 的取值范围;
的取值范围;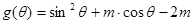 ,若集合
,若集合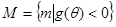 ,集合
,集合 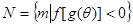 ,求
,求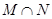
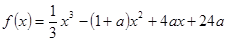 ,其中常数
,其中常数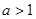
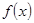 的单调性
的单调性 时,
时,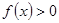 恒成立,求
恒成立,求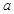 的取值范围
的取值范围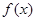 在区间
在区间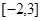 是增函数,则
是增函数,则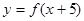 的递增区间是 ( )
的递增区间是 ( )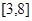
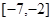

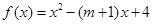 .
.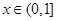 时,若
时,若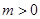 ,求函数
,求函数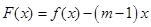 的最小值;
的最小值;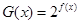 的图象与直线
的图象与直线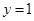 恰有两个不同的交点
恰有两个不同的交点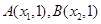
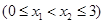 ,求实数
,求实数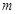 的取值范围.
的取值范围. 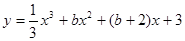 是R上的单调增函数,则
是R上的单调增函数,则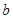 的取值范围是
的取值范围是