一堆零件堆积如图所示.自上而下第1层1个.第2层个.-.求第n层个数. 题目和参考答案——青夏教育精英家教网—

题目内容

一堆零件堆积如图所示，自上而下第1层1个，第2层（1+2）个，第3层（1+2+3）个，…，求第n层个数.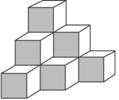

试题答案

相关练习册答案

思路解析：依题意，第k层有1+2+3+…+k=12k（k+1）个，它是k的二次三项式.

解：因为a_k=1+2+…+k=k²+k.

所以S_n=1+（1+2）+（1+2+3）+…+（1+2+…+n）

=（1²+2²+3²+…+n²）+（1+2+…+n）

=n（n+1）（2n+1）+n（n+1）

=n（n+1）［（2n+1）+3］

=n（n+1）（n+2）.

评注：本题的求和方法是从通项“a_k=k²+k”找到解题的突破口，利用了公式“1²+2²+…+n²=n（n+1）（2n+1）”.这种数列求和的方法经常用到.

练习册系列答案

乐知源现代文阅读系列答案

试题分类